147. Задания для самостоятельной работы № 23
Ответьте на вопросы
1. Назовите формулы для вычисления площади криволинейной трапеции.
2. Как найти площадь любой плоской фигуры в прямоугольной системе координат?
3. Как найти объем тела при помощи определенного интеграла?
4. Чему равен объем тела вращения?
5. Как найти длину дуги плоской кривой?
6. Какой формулой определяется площадь поверхности вращения?
Самостоятельная работа № 23
I. Найдите неопределенные интегралы.
1) ![]() ; 2)
; 2) 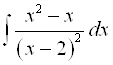 ; 3)
; 3) 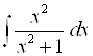 ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
7) ![]() ; 8)
; 8) ![]() .
.
II. Вычислите определенные интегралы.
1) 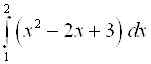 ; 2)
; 2) 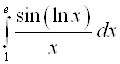 ; 3)
; 3) 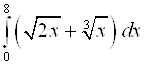 ;
;
4) 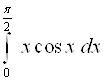 ; 5)
; 5) 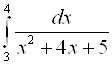 ; 6)
; 6) 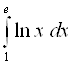 .
.
III. Вычислите площади плоских фигур, ограниченных линиями:
1) кривой 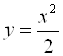 и прямыми линиями
и прямыми линиями ![]() и
и ![]() ;
;
2) кривой ![]() и осью Оу;
и осью Оу;
3) кривой ![]() и кривой
и кривой ![]() ;
;
4) кривой ![]() , прямой
, прямой ![]() , и осью Оу;
, и осью Оу;
5) прямой ![]() и кривой
и кривой ![]() .
.
IV. Найдите объем тела, образованного вращением фигур, ограниченных линиями:
1) ![]() и
и ![]() вокруг оси Ох;
вокруг оси Ох;
2) 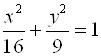 вокруг оси Оу;
вокруг оси Оу;
3) ![]() и
и ![]() вокруг оси Ох.
вокруг оси Ох.
V. Найдите длину дуги плоской кривой:
1) ![]() от начала координат до точки
от начала координат до точки ![]() ;
;
2) ![]() от
от ![]() до
до ![]() ;
;
3) ![]() от
от ![]() до
до ![]() ;
;
4) 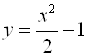 , ограниченной осью Ох.
, ограниченной осью Ох.
VI. Найдите площадь поверхности вращения:
1) эллипса ![]() вокруг оси Оу;
вокруг оси Оу;
2) дуги окружности ![]() вокруг оси Оу между точками, где
вокруг оси Оу между точками, где ![]() ,
, ![]() ;
;
3) дуги параболы ![]() вокруг оси Ох между точками пересечения ее с прямой
вокруг оси Ох между точками пересечения ее с прямой ![]() .
.
| < Предыдущая | Следующая > |
|---|