134. Общая схема исследования функций и построение графиков

Для проведения полного исследования функции и построения ее графика необходимо использовать определения интервалов монотонности функций, экстремумов функции, интервалов выпуклости и вогнутости графика, его точек перегиба и асимптот. Такой график не будет очень точным, но он позволяет отметить основные свойства и особенности исследуемой функции.

Полное исследование функции проводим по следующей схеме.

1. Находим область определения и точки разрыва функции.

2. Определяем четность, нечетность функции.

3. Определяем нули функции (точки, в которых функция равна нулю).

4. Определяем интервалы положительности и отрицательности функции (по нулям функции и точкам разрыва).

5. Определяем асимптоты графика:

А) вертикальные , если ;

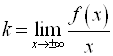Б) наклонные , где и .

6. Устанавливаем периодичность функции.

7. Находим критические точки первой производной и точки ее разрыва (точки, в которых , или первая производная не существует).

8. Находим интервалы возрастания () или убывания () функции (по критическим точкам первой производной).

9. Исследуем критические точки на экстремум (по изменению знака производной при переходе через критическую точку).

10. Определяем значения функции в точках экстремума.

11. Находим точки разрыва и нули второй производной.

12. Находим интервалы выпуклости () или вогнутости () функции (по критическим точкам второй производной).

13. Находим точки перегиба (по изменению знака второй производной при переходе через критическую точку).

14. Наносим на график полученные результаты.

Для большей точности построения графика рекомендуется вычислить значения функции в дополнительных точках и нанести их на координатную плоскость.

Исследуем функцию по приведенной схеме.

Пример 9. Исследуйте функцию и постройте ее график.

Решение. 1. Знаменатель этой дроби обращается в ноль () при , значит, в этой точке функция не определена.

Областью определения функции есть вся числовая ось, кроме точки : .

Точка – это точка разрыва функции. При подходе к точке слева, всегда будет оставаться меньше , а значит знаменатель , и числитель . Тогда: .

При подходе к точке справа, всегда будет больше , и значит и . Тогда: .

2. Для этой функции не выполняется условие четности и условие нечетности . Значит, это функция общего вида.

3. Функция обращается в ноль, если ее числитель равен нулю . Тогда: . В точке функция равна нулю.

4. Определим интервалы положительности, отрицательности, исследуя поведение функции в точке разрыва и точке , в которой функция обращается в ноль.

Слева от точки функция всегда отрицательна, а справа положительна. На интервале функция отрицательна, а на интервале функция положительна. При переходе через точку функция знак не меняет и остается положительной.

5. Уравнением вертикальной асимптоты будет , так как

и .

Запишем уравнение наклонной асимптоты и найдем:

,

.

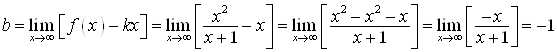Уравнение наклонной асимптоты будет таким: .

6. Функция непериодическая.

7. Найдем производную функции: .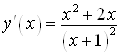

Критические точки первой производной определим из следующих условий:

– первая производная обращается в ноль, если . Решением этого уравнения будут две точки и ;

– первая производная не существует, если . Решением этого уравнения будет точка .

Точка – это точка разрыва производной, и она совпадает с точкой разрыва функции .

Точка совпадает с точкой , в которой функция обращается в ноль. Таким образом, для функции и ее первой производной имеем три критические точки: , , .

В точке функция и ее первая производная не существуют, потому что – это точка разрыва функции и ее производной.

В точке : и .

В точке : , а .

8. Рассмотрим интервалы между критическими точками и определим знак производной внутри каждого интервала. Для удобства работы составим таблицу 11.4.

Для определения знака производной возьмем по одной точке из каждого интервала и вычислим значение производной в этой точке.

Из интервала возьмем точку , получим

Из интервала возьмем точку , получим .

Из интервала возьмем точку , получим .

Из интервала возьмем точку , получим .

Таблица 11.4 – Исследование функции и ее производной

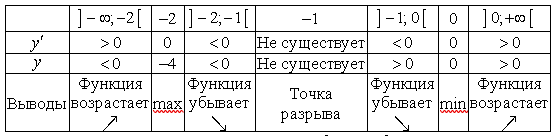
Из таблицы видно, что на интервале функция возрастает, , на интервале функция убывает, , и на интервале функция вновь возрастает, .

9. Из таблицы 11.4 видно, что при переходе через критическую точку первая производная меняет знак с "плюса" на "минус". Значит, в точке находится экстремум (максимум) функции.

В точке производная и сама функция не существуют. Это точка разрыва функции.

При переходе через точку первая производная меняет знак с "минуса" на "плюс". Значит, точке находится экстремум (минимум) функции.

10. Найдем значения функции в точках экстремума:

, .

11. Найдем вторую производную функции: .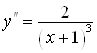

ни при каких значениях переменной , а в точке вторая производная не существует, так как знаменатель дроби обращается в ноль. Значит, в критической точке будет разрыв второй производной.

12. Для второй производной имеется только одна критическая точка , поэтому рассмотрим два интервала изменения знака второй производной.

В интервале вторая производная . Следовательно, график функции выпуклый.

В интервале вторая производная . Следовательно, график функции вогнутый.

13. Точек перегиба нет, так как вторая производная ни при каких значениях переменной не обращается в ноль.

14. Дополним таблицу 11.4 результатами анализа второй производной, получим таблицу 11.5.

Таблица 11.5 – Исследование функции и ее производных

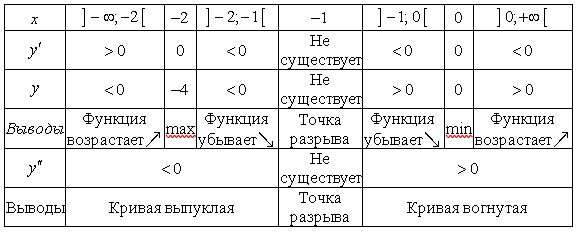
Для более точного построения графика вычислим значения функции в дополнительных точках (табл. 11.6).

Таблица 11.6 – Значения функции в дополнительных точках

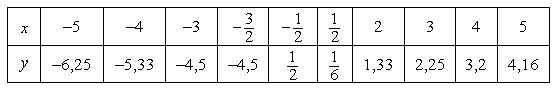
Построим асимптоты функции и по результатам, представленным в таблицах 11.5 и 11.6 построим график функции (рис. 11.13).

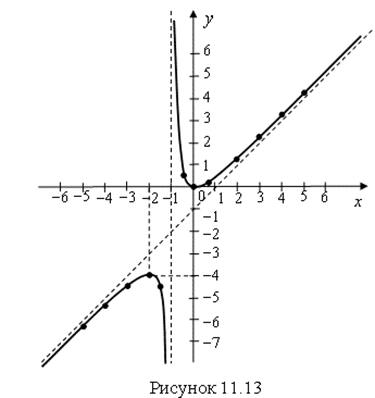
Ответ. График функции изображен на рисунке 11.13.

< Предыдущая		Следующая >