133. Асимптоты графика
Асимптоты графика ![]() могут быть вертикальные (параллельные оси Oу) и невертикальные (горизонтальные и наклонные). Вертикальных асимптот может быть много. Например, для функции
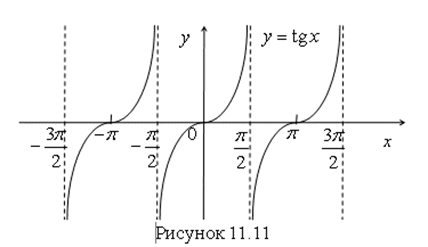
могут быть вертикальные (параллельные оси Oу) и невертикальные (горизонтальные и наклонные). Вертикальных асимптот может быть много. Например, для функции ![]() их бесконечное число (рис. 11.11).
их бесконечное число (рис. 11.11).
Если ![]() , то прямая
, то прямая ![]() – это Вертикальная Асимптота графика.
– это Вертикальная Асимптота графика.
Например, на рисунке 11.11 прямые вида 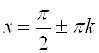 – это вертикальные асимптоты графика функции
– это вертикальные асимптоты графика функции ![]() .
.
Невертикальных асимптот не может быть больше двух (одна при ![]() и вторая при
и вторая при ![]() ).
).
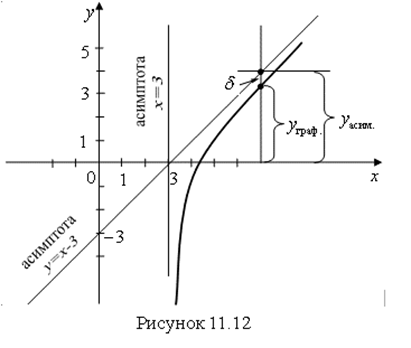
Если прямая ![]() есть асимптота графика
есть асимптота графика ![]() при
при ![]() , то
, то ![]() и когда
и когда ![]() стремится к бесконечности, то
стремится к бесконечности, то ![]() стремится к нулю (рис. 11.12).
стремится к нулю (рис. 11.12).
Из условия ![]() найдем значение углового коэффициента
найдем значение углового коэффициента ![]() .
.
Разделив правую и левую часть равенства на ![]() получим
получим 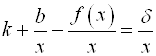 , тогда
, тогда 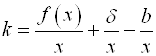 .
.
Найдем предельное значение этого выражения при ![]()
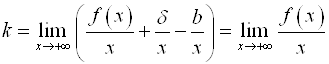 .
.
Теперь из уравнения ![]() найдем
найдем ![]() .
.
Предельное значение B При ![]() будет равно:
будет равно:
![]() .
.
Если существуют эти пределы и они конечны, то прямая ![]() является асимптотой графика функции
является асимптотой графика функции ![]() . Если такие пределы не существуют, то невертикальных асимптот нет.
. Если такие пределы не существуют, то невертикальных асимптот нет.
Аналогично можно показать, что если функция ![]() определена на интервале
определена на интервале ![]() , то
, то 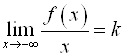 а
а ![]() . Прямая
. Прямая ![]() называется Наклонной асимптотой, если
называется Наклонной асимптотой, если ![]() . Если
. Если ![]() , то прямая
, то прямая ![]() называется Горизонтальной асимптотой.
называется Горизонтальной асимптотой.
Пример 8. Найдите асимптоты графика функции 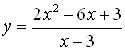 .
.
Решение. Областью определения функции будет вся числовая ось, кроме точки ![]()
![]() .
.
В точке ![]() есть бесконечный разрыв. Прямая
есть бесконечный разрыв. Прямая ![]() это вертикальная асимптота.
это вертикальная асимптота.
Уравнение невертикальных асимптот находим по формуле: ![]() где
где 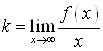 ,
, ![]() . Получим:
. Получим:
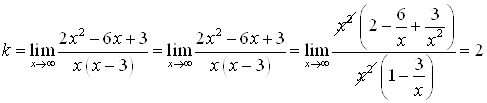 ;
; 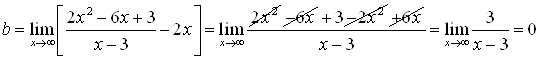 .
.
Тогда уравнение наклонной асимптоты будет ![]() .
.
Ответ: Вертикальная асимптота ![]() ; наклонная асимптота
; наклонная асимптота ![]() .
.
Ответьте на вопросы
1. При каких условиях график функции будет иметь вертикальные асимптоты?
2. Сколько вертикальных асимптот может иметь график функции ![]() ?
?
3. Каково условие существования невертикальных (наклонных) асимптот?
4. Напишите формулу углового коэффициента K для наклонной асимптоты функции ![]() .
.
5. Напишите формулу свободного члена B для наклонной асимптоты функции ![]() .
.
6. Сколько невертикальных (наклонных) асимптот может иметь график функции ![]() ?
?
7. Напишите формулу горизонтальной асимптоты.
| < Предыдущая | Следующая > |
|---|