131. Выпуклость или вогнутость кривой. Точки перегиба графика функции
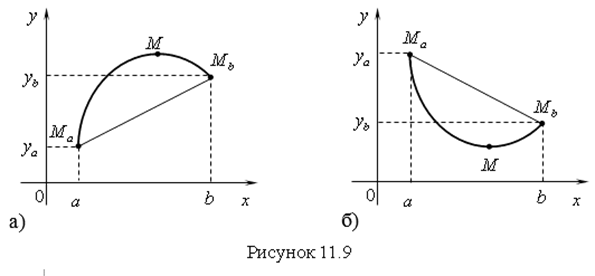
Кривая графика функции называется Выпуклой вверх (Выпуклой) на интервале 
, если точки кривой лежат над хордой 
(рис. 11.9 а).
Кривая графика функции называется Выпуклой вниз (Вогнутой) на интервале , если точки кривой лежат под хордой (рис. 11.9 б).
Напомним, что Хорда – это отрезок, который соединяет две точки графика функции.
Теорема. Если кривая 
Выпуклая на интервале 
, то на этом интервале ее вторая производная отрицательна, 
.
Если кривая 
вогнутая На интервале , то на этом интервале ее вторая производная положительна, 
.
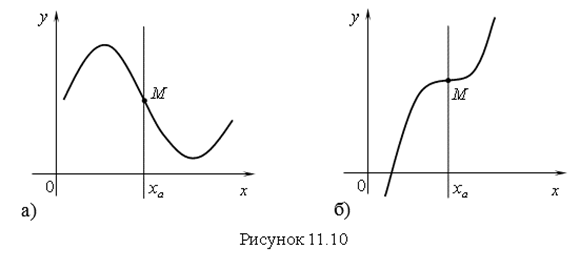
Точка, которая отделяет выпуклую часть от вогнутой, называется Точкой Перегиба (рис. 11.10). В точке перегиба вторая производная равна нулю и меняет знак при переходе через эту точку.
Чтобы исследовать функцию на выпуклость, вогнутость и точки перегиба, необходимо:
1) найти область определения и интервалы, на которых функция непрерывна;
2) найти вторую производную функции и внутренние точки области определения, в которых 
или не существует;
Найти знак второй производной функции и исследовать характер поведения функции на полученных интервалах.
Пример 4. Найдите точку перегиба и исследуйте на выпуклость, вогнутость график кривой 
.
Решение. 1. Найдем область определения функции 
2. Найдем первую и вторую производные функции:
;
.
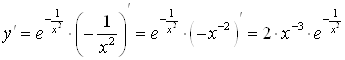Вторая производная 
в точке 
и не существует, когда 
. Значит, при 
Функция 
не определена.
3. Полученные точки разбивают область определения функции на интервалы: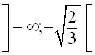 
, 
, 
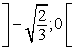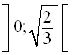и 
. И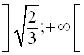сследуем знаки второй производной на этих интервалах и результаты занесем в таблицу 11.3.
Множители 
и 
на всей области определения, поэтому знак второй производной будет определять только множитель 
. Исследуем знак множителя на каждом из интервалов.
А) Найдем знак второй производной на интервале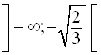 
. Для этого подставим значение 
из данного интервала в множитель . Получим, что 
. Следовательно, 
и кривая графика будет выпуклой.
Б) Найдем знак второй производной на интервале 
. Для этого подставим значение 
из данного интервала в множитель . Получим, что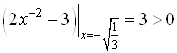 
. Следовательно, 
и кривая графика будет вогнутой.
В) Найдем знак второй производной на интервале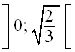 
. Для этого подставим значение 
из данного интервала в множитель . Получим, что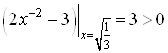 
. Следовательно, и кривая графика будет вогнутой.
Г) Найдем знак второй производной на интервале 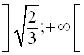. Для этого подставим значение 
из данного интервала в множитель . Получим, что 
. Следовательно, и кривая графика будет выпуклой.
Таблица 11.3 – Исследование функции и ее производной
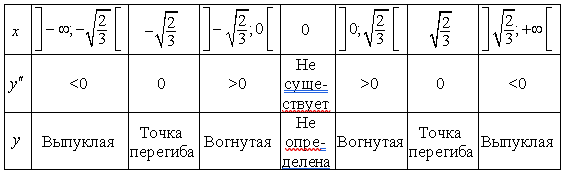
При переходе через точки 
и 
вторая производная меняет знак. Эти точки есть точки перегиба.
Ответ. На интервалах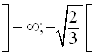 
и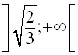 
функция выпуклая. На интервалах 
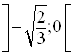и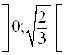 
функция вогнутая. Точки 
и 
– это точки перегиба.
Ответьте на вопросы
1. Какая кривая графика на интервале 
называется выпуклой, а какая – Вогнутой?
2. Какая точка графика функции называется точкой перегиба?
3. Какой знак имеет вторая производная, если кривая графика функции на интервале выпуклая, вогнутая?
| < Предыдущая | Следующая > |
|---|
