130. Наибольшее и наименьшее значение функции на интервале

Пусть функция непрерывна в замкнутом интервале и пусть в этом же интервале непрерывна ее первая производная. Необходимо найти наибольшее и наименьшее значения функции на этом интервале.

Для решения задачи недостаточно знать только экстремумы функции, необходимо учитывать и значения функции на краях интервала.

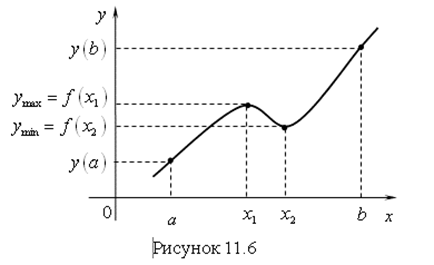
Из рисунка 11.6 видно, что экстремумами функции в интервале будут значения функции в точках и . Но это не наибольшее и наименьшее значения в интервале.

Здесь наибольшим будет значение функции на краю интервала при , , а наименьшим будет значение функции на другом краю интервала при , .

Теорема 1. Если в некотором интервале (конечном или бесконечном) функция непрерывна и имеет только один экстремум, и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции на этом интервале (рис. 11.7 а, б).

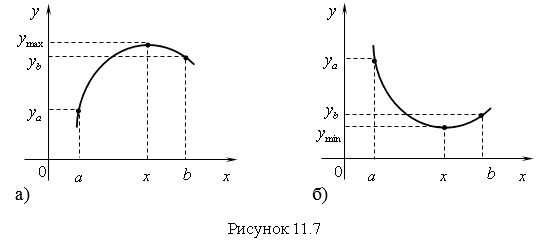
На рисунке 11.7 а и 11.7 б показаны графики функций, имеющие один экстремум на конечном или бесконечном интервале.

Теорема 2. Если функция непрерывна на отрезке , то она обязательно имеет на этом интервале наибольшее и наименьшее значения. Эти значения будут или в точках экстремума или на концах интервала.

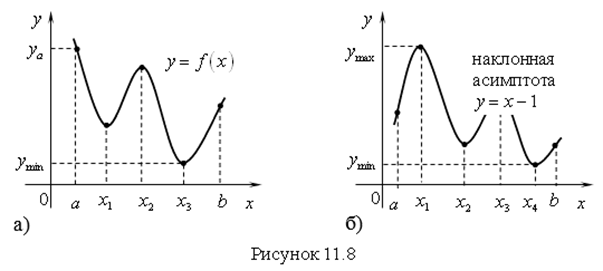
Наибольшее значение функция принимает на конце интервала , а наименьшее значение – внутри интервала (рис. 11.8 а).

Функция принимает наибольшее значение в точке экстремума , а наименьшее значение в точке экстремума (рис. 11.8 б).

Для того, чтобы найти наибольшее и наименьшее значения функции на интервале , необходимо:

1) найти критические точки функции, которые принадлежат данному интервалу;

2) найти значения функции в критических точках;

3) найти значения функции на краях интервала;

Сравнить полученные результаты и найти наибольшее и наименьшее значения функции на интервале.

Пример 3. Найдите наибольшее и наименьшее значения функции на интервале .

Решение. Данная функция непрерывна в заданном интервале и имеет первую производную , значит, в этом интервале она имеет наибольшее и наименьшее значения (согласно теореме 2). Найдем эти значения.

1. Критическими точками этой функции будут точки, в которых ее первая производная обращается в нуль . Приравняем производную к нулю и решим полученное уравнение: , . В этих точках данная функция имеет экстремумы.

2. Найдем значения функции в критических точках: ; .

3. Найдем значения функции в точках и , т. е. на краях интервала:

4. Сравним полученные значения функции в критических точках и на краях интервала . Получим, что наименьшее значение функция принимает на краю интервала при , а наибольшее значение соответствует критической точке .

Ответ. ; .

Ответьте на вопросы

1. Где может находиться наименьшее или наибольшее значение непрерывной на интервале функции?

2. Если непрерывная функция в точке имеет один min на интервале , то где будет наименьшее значение функции и чему оно будет равно?

3. Как найти наибольшее и наименьшее значение функции на интервале ? Назовите порядок действий.

< Предыдущая		Следующая >