129. Точки экстремума

Если при некотором значении значение больше (меньше) всех "соседних" значений функции, то точка называется точкой Максимума (Минимума), а значение функции в этой точке называется Максимальным (Минимальным) значением функции.

Точки максимума и минимума называются Точками экстремума.

Значения функции в точках максимума и минимума называются Экстремумами функции (максимумом и минимум функции).

Необходимое условие экстремума. В точках экстремума производная функции либо равна нулю, либо не существует, т. е. если – это точка экстремума, то или – не существует. (Но не в каждой точке будет экстремум, если или – не существует!)

Достаточное условие экстремума. Если функция непрерывна в точке , и производная меняет знак при переходе через точку , то точка – это точка экстремума функции .

Если при переходе через точку первая производная функции меняет знак с "+" на "–", тогда – это точка максимума.

Если при переходе через точку первая производная функции меняет знак с "–" на "+", тогда – это точка минимума.

Точки экстремума – это стационарные точки. Но не всегда стационарные точки являются точками экстремума.

Например, в предыдущей задаче точка является точкой экстремума функции (точкой минимума), так как при переходе через эту точку производная меняет знак с "–" на "+".

Внутренние точки области определения функции, в которых производная функции равна нулю или не существует, называются Критическими точками.

Для исследования функции на экстремум необходимо:

1) найти область определения функции;

2) найти первую производную функции;

3) найти критические точки функции;

4) найти интервалы возрастания и убывания функции;

5) проверить изменение знака производной при переходе через критические точки;

Вычислить значение функций в точках экстремума.

Пример 2. Исследуйте на экстремум функцию .

Решение. Областью определения функции будет вся числовая ось. Точек разрыва функции нет.

1. Найдем точки пересечения функции с осью Ох. Если , то , , .

2. Найдем первую производную функции: .

3. Приравняем производную к нулю: . Получим: , . Полученные точки являются критическими точками.

4. Для определения интервалов возрастания и убывания составим таблицу и найдем знак производной на каждом из интервалов и в критических точках.

А) Определим знак производной в точке из интервала :

.

Б) Определим знак производной в точке из интервала :

.

В) Определим знак производной в точке из интервала :

.

Все полученные результаты внесем в таблицу 11.2.

Таблица 11.2 – Исследование функции и ее производной

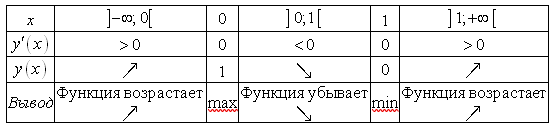
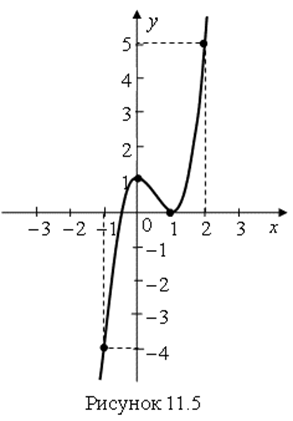
Используя данные таблицы 11.2, дополним их значениями и . Нанесем полученные точки на график (рис. 11.5).

Как видно из таблицы 11.2 и рисунка 11.5, функция возрастает в интервалах и , где ее производная положительна и убывает в интервале , где ее производная отрицательна.

5. Определим значение функции в точках и , при переходе через которые производная меняет знак: .

При переходе через точку производная меняет знак с плюса на минус. В этой точке функция имеет максимум .

При переходе через точку производная меняет знак с минуса на плюс. В этой точке функция имеет минимум .

Ответ. Функция имеет максимум в точке и минимум в точке .

Ответьте на вопросы

1. Какие точки графика функции называются точками экстремума?

2. Какое необходимое условие экстремума?

3. Назовите достаточное условие экстремума.

4. Какие точки называются критическими точками?

5. Как исследовать функцию на экстремум?

< Предыдущая		Следующая >