128. Интервалы монотонности

Функция дифференцируема на отрезке , если она дифференцируема в каждой точке отрезка. В этом случае производная тоже есть функция от : .

В точке разрыва функция не может иметь производной. Если функция Дифференцируема в точке , то она в этой точке Непрерывна.

Если функция в точке не имеет производной, это значит, что в этой точке на графике функции не существует касательной, или эта касательная образует с осью угол 90°.

Если для данной точки производная не существует, то есть не существует предел в этой точке, но существуют пределы слева и справа, то эти пределы называют Производной слева и Производной справа .

Пусть функция непрерывна в интервале и имеет производную в этом интервале. Производная такой функции в точке из этого интервала будет равна тангенсу угла наклона касательной к оси Ох.

Для того, чтобы эта функция на интервале была постоянна , необходимо и достаточно выполнить условие равенства нулю производной во всех точках этого интервала.

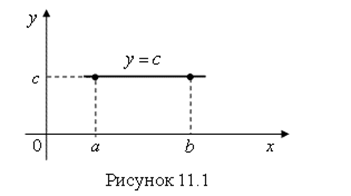
Графиком постоянной функции будет прямая, параллельная оси абсцисс (рис. 11.1). Угол наклона касательной в каждой точке данного графика равен нулю, а значит и , и производная функции в каждой точке графика равна нулю.

Для того чтобы функция Возрастала на интервале , необходимо, чтобы ее первая производная была положительна в каждой точке интервала.

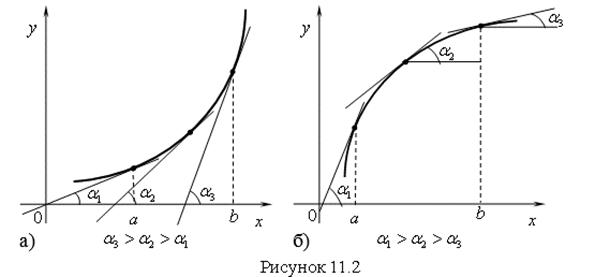
Как мы видим из рисунка 11.2, если функция возрастает на интервале , то угол наклона касательной будет изменяться от 0˚ до 90˚.

При изменении угла наклона в интервале будет всегда больше нуля.

Для того, чтобы функция Убывала на интервале , необходимо и достаточно, чтобы ее первая производная на этом интервале была отрицательна ().

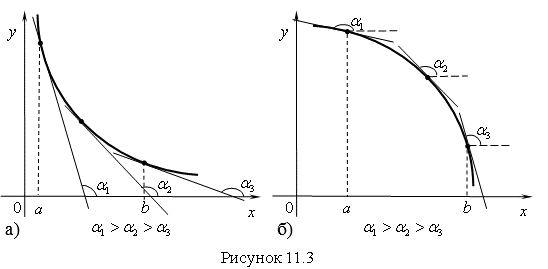
Анализируя рисунки 11.3 а и 11.3 б можно определить, что угол наклона касательной изменяется в интервале . При изменении угла от 90˚ до 180˚ будет всегда отрицательным.

Условие монотонности функции

Дифференцируемая во всей области определения функция возрастает на каждом интервале, в котором ее производная положительна и убывает на каждом интервале, в котором ее производная отрицательна.

Функция возрастает, если скорость ее изменения положительна и функция убывает, если скорость ее изменения отрицательна.

Если производная на интервале переходит от положительных значений к отрицательным или от отрицательных к положительным, то она должна пройти через нулевое значение.

Точки, в которых значение производной равно нулю, называются Стационарными точками.

Чтобы найти интервалы монотонности функции (интервалы возрастания или убывания), необходимо:

1) найти точки, в которых функция обращается в ноль ;

2) найти первую производную функции ;

3) найти стационарные точки из условия, что ;

4) нанести эти точки на ось и проверить знак производной на каждом интервале между соседними стационарными точками.

Пример 1. Найдите интервалы возрастания и убывания функции .

Решение. 1. Найдем точки, в которых функция обращается в ноль, то есть , тогда ; .

2. Найдем первую производную функции , получим .

3. Найдем стационарные точки из условия , тогда , откуда .

4. Нанесем полученные точки на ось Ох и проверим знак производной в каждом из полученных интервалов.

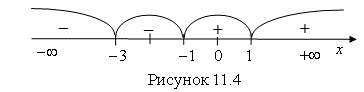
Возьмем точку , которая принадлежит интервалу и определим значение производной в этой точке: , значит, функция убывает на этом интервале.

Возьмем точку из интервала , тогда , значит, функция убывает на этом интервале.

Возьмем точку из интервала , тогда , значит, функция возрастает на этом интервале.

Возьмем точку из интервала , тогда , значит, функция возрастает на этом интервале.

Для удобства анализа поведения функции составим таблицу 11.1, в которую запишем все полученные данные.

Таблица 11.1 – Исследование функции и ее производной

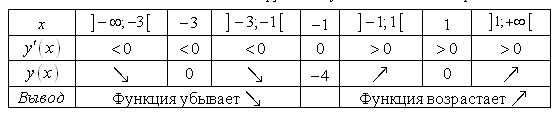
Из таблицы 11.1 видно, что функция убывает на интервале и возрастает на интервале .

В стационарной точке производная .

Ответ. Функция убывает на интервале и возрастает на интервале .

Ответьте на вопросы

1. Что обозначают термины: производная слева, производная справа?

2. Назовите условие, при котором функция будет постоянна на интервале.

3. При каких значениях производной функция возрастает на интервале?

4. При каких значениях производной функция убывает на интервале?

5. Какие точки графика функции называются стационарными точками?

6. Как найти интервалы монотонности функции?

< Предыдущая		Следующая >