124. Дифференциал функции

Рассмотрим график функции (рис. 10.4).

В точке М (Х0,У0) значение функции будет равно . Дадим аргументу функции приращение (отрезок МК). Значение функции в точке будет равно , а ее приращение . На чертеже это отрезок NK.

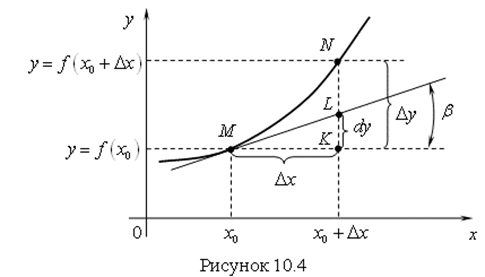
Найдем значение производной функции в точке М. Значение производной, как мы знаем, равно тангенсу угла наклона касательной к графику функции в данной точке . Эта касательная отсекает на отрезке NK отрезок KL, который составляет часть приращения функции. Эту часть приращения функции обозначают и называют Дифференциалом функции.

Тогда 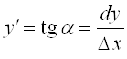, откуда мы получим: .

Для линейной функции имеем . Дифференциал аргумента равен его приращению. Но тогда , и мы получаем обозначение производной .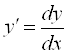

Главная часть приращения функции, которая линейна относительно , называется дифференциалом функции:

.

Если в формуле приращения функции заменить на значение дифференциала в этой точке, то можно записать приближенное равенство . Тогда получим:

.

Эта формула позволяет приближенно вычислить значение функции, если аргумент получает небольшие приращения.

Пример 18. Найдите приближенное значение функции в точке , если приращение функции заменить его дифференциалом.

Решение. Принимаем первоначальное значение функции в точке . Тогда , а , .

Приближенное значение функции в точке найдем по формуле . Получим: . Если мы вычислим точно значение функции при , то . Погрешность составляет 0,01.

Ответ.

Пример 19. Вычислить приближенно .

Решение. Запишем задание в виде функции . Пусть начальное значение переменной будет , тогда , а . Таким образом, значение производной функции будет равно: . Если , тогда найдем значения производной: .

Если , тогда значение функции будет равно:

.

Найдем значения функции с точностью до при помощи калькулятора: .

Погрешность результата составляет: d = 0,0004569.

Ответ. .

Пример 20. Найдите .

Решение. Для функции при имеем: ,

,

,

.

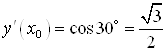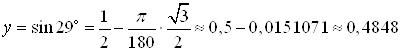Ответ. .

Дифференциал второго порядка – это дифференциал от дифференциала первого порядка. Для функции в дифференциале первого порядка при повторном дифференцировании считается независимым от Х, и дифференциал второго порядка будет записан так:

.

Аналогично можно записать Дифференциал n - го порядка в виде: .

Ответьте на вопросы

1. Какая часть приращения функции называется дифференциалом?

2. Чему равен дифференциал аргумента?

3. Как связан дифференциал и производная функции?

4. Как записать дифференциал N - го порядка?

5. Прочитайте формулу .

6. Прочитайте формулу .

< Предыдущая		Следующая >