123. Производные высших порядков
Пусть функция ![]() имеет производную
имеет производную ![]() , которая тоже есть функция от
, которая тоже есть функция от ![]() . Тогда эту производную мы называем Производной Первого порядка или Первой производной. Но от полученной первой производной (функции) мы так же можем взять производную, которая будет называться Производной второго порядка Или Второй производной:
. Тогда эту производную мы называем Производной Первого порядка или Первой производной. Но от полученной первой производной (функции) мы так же можем взять производную, которая будет называться Производной второго порядка Или Второй производной: ![]() .
.
Аналогично можно найти производные третьего, четвертого, … N-го порядка. Производные высших порядков обозначаются так:
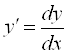 – производная первого порядка ("Де игрек по де икс");
– производная первого порядка ("Де игрек по де икс");
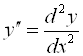 – производная второго порядка ("Де два игрек по де икс дважды");
– производная второго порядка ("Де два игрек по де икс дважды");
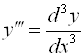 – производная третьего порядка ("Де три игрек по де икс трижды");
– производная третьего порядка ("Де три игрек по де икс трижды");
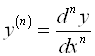 – производная N-го порядка ("Де эн игрек по де икс эн").
– производная N-го порядка ("Де эн игрек по де икс эн").
Пример 14. Найдите пятую производную функции ![]() .
.
![]()
Ответ. ![]() .
.
Если Y=U+V+…+W, то ее энная производная равна сумме энных производных функций U, V…W:
![]() .
.
Формула для производной произведения ![]() может быть записана в виде формулы Лейбница:
может быть записана в виде формулы Лейбница:
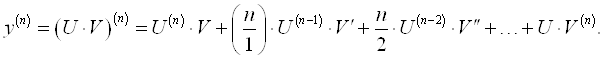
Используя производные высших порядков, дифференцируемую функцию можно представить в виде многочлена N–ой степени.
Теорема Тейлора. Функция, дифференцируемая N+1 раз в некотором интервале, который содержит точку ![]() , может быть представлена в виде многочлена N–ой степени и остаточного члена
, может быть представлена в виде многочлена N–ой степени и остаточного члена ![]() :
:
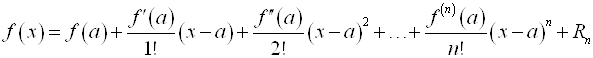 ,
,
Где 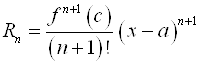 есть остаточный член разложения
есть остаточный член разложения
Можно показать, что остаточный член имеет более высокий ![]() порядок малости по сравнению с
порядок малости по сравнению с ![]() и функцию, которая задается одной формулой на всех участках изменения аргумента можно разложить в ряд Тейлора.
и функцию, которая задается одной формулой на всех участках изменения аргумента можно разложить в ряд Тейлора.
Числовым рядом называется бесконечное выражение вида
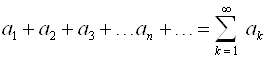 ,
,
Где ![]() называются членами ряда.
называются членами ряда.
Функции, заданные на одном и том же отрезке ![]() , называются Функциональными рядами.
, называются Функциональными рядами.
Разложим функцию ![]() по степеням
по степеням ![]() , используя формулу Тейлора:
, используя формулу Тейлора: 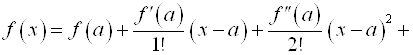
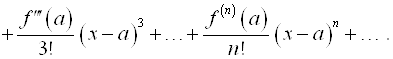
![]()
Если в формуле разложения функции по степеням положить А = 0, то мы имеем:
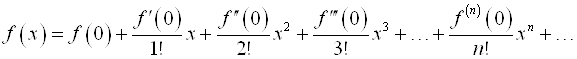 .
.
Пример 15. Разложите в ряд по степеням ![]() функцию
функцию ![]() .
.
Решение. Найдем производные этой функции: ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() .
.
![]() .
.
![]() .
.
По этой формуле можно приближенно вычислить число ![]() с любой степенью точности.
с любой степенью точности.
![]() .
.
Ответ. Для ![]() .
.
Для ![]() .
.
Для ![]() .
.
Пример 16. Разложите в ряд по степеням х функцию ![]() .
.
Решение. Найдем ![]() .
.
Найдем первые семь производных функции при ![]() :
:
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
Запишем первые восемь членов разложения функции ![]() :
:
![]() ,
,
Или 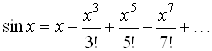 .
.
Ответ. 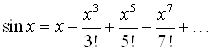 .
.
Пример 17. Разложите в ряд по степеням ![]() функцию
функцию ![]() .
.
Решение. Найдем ![]() .
.
Найдем первые семь производных и их значения при ![]() :
:
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
Запишем первые восемь членов ряда разложения:
![]() ,
,
Или 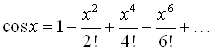 .
.
Ответ. 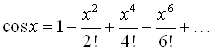 .
.
Аналогично можно получить разложения других элементарных функций.
Ответьте на вопросы
1. Что такое производная второго порядка?
2. Как найти производную третьего порядка?
3. Напишите формулу N-й производной суммы функций ![]() .
.
4. Напишите формулу N-й производной произведения функций ![]() .
.
5. Как разложить функцию ![]() в ряд по степеням
в ряд по степеням ![]() ?
?
6. Напишите формулы разложения функций ![]() ,
, ![]() и
и ![]() по степеням
по степеням ![]() .
.
7. Сформулируйте теорему Тейлора.
8. Что такое числовой ряд?
9. Что такое функциональный ряд?
| < Предыдущая | Следующая > |
|---|