122. Производные основных элементарных функций. Свойства производной

Таблица 10.1 – Производные основных элементарных функций

Рассмотрим некоторые свойства производной.

1. Производная постоянной равна нулю: .

Если У = С, то ∆У = С – С = 0, а .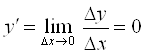

Пример 3. Найдите производную функции .

Решение. По формуле найдем: .

Ответ. .

2. Постоянный множитель можно вынести за знак производной: .

Если то

, а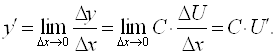

Пример 4. Найдите производную функции .

Решение. Перепишем функцию: . Найдем производную: .

Ответ. .

3. Производная суммы функций равна сумме производных этих функций: .

Если то

.

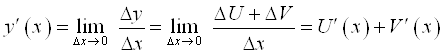Пример 5. Найдите производную функции .

Решение. .

Ответ. .

4. Производная произведения функций:

.

Если то

, тогда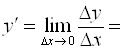

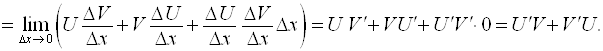
Пример 6. Найдите производную функции .

Решение. Обозначим и . Используем формулу производной произведения функций , получим: .

Ответ. .

5. Производная частного двух функций: .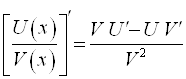

Если 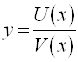, то ,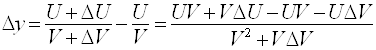

.

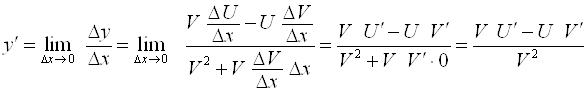Пример 7. Найдите производную функции .

Решение. Обозначим и . Используем формулу производной частного двух функций:

.

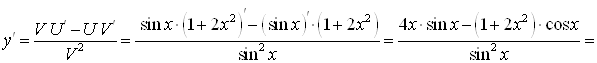
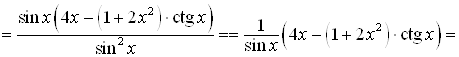
Ответ. .

6. Производная сложной функции: .

Если , где , то есть сложная функция.

Если аргумент х получает приращение ∆Х, то U(Х) получает приращение ΔU, а функция получает приращение ΔУ. При этом 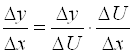, а значит 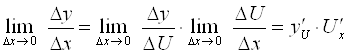, так как при ΔХ → 0, ΔU → 0.

Пример 8. Найдите производную функции .

Решение. Обозначим . Используем формулу производной сложной функции:

Ответ. .

Пример 9. Найдите производную функции .

Решение. Обозначим . Используем формулу производной сложной функции:

Ответ. .

7. Производная обратной функции: .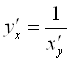

Пусть равенство У = У (Х) имеет (определяет) обратную зависимость , для которой мы можем найти производную . Тогда легко найти и производную от исходной функции. Действительно, 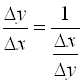, откуда при и получаем .

Пример 10. Найдите производную .

Решение. Запишем обратную функцию . Найдем ее производную
по , получим: . Сравним это выражение с производной от по : .

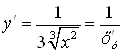Ответ. .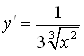

8. Производная неявной функции.

Если задана неявная функция , то для вычисления производной нужно приравнять производные от левой и правой частей, считая, что есть функция от , которая обращает соотношение в тождество.

Пример 11. Найдите производную функции , заданную соотношением .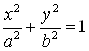

Решение. 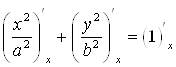, , тогда или .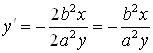

Ответ.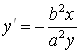

9. Логарифмическое дифференцирование.

Иногда, прежде чем находить производную, удобно прологарифмировать функцию.

Пример 12. Найдите производную функции .

Решение. Прологарифмируем обе части равенства .

Дифференцируем обе части равенства:

, откуда .

Ответ. .

Пример 13. Найдите производную функции .

Решение. ; ;

;

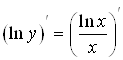Ответ. .

Ответьте на вопросы

1. Напишите формулу производной степенной функции.

2. Чему равна производная функции ?

3. Напишите формулы производных тригонометрических функций.

4. Чему равна производная показательной функции ?

5. Напишите формулы производных обратных тригонометри-ческих функций.

6. Напишите формулу производной функции.

7. Напишите формулу производной суммы функций.

8. Как прочитать формулу ?

9. Как прочитать формулу ?

10. Как найти производную неявной функции?

11. Как называется функция ?

< Предыдущая		Следующая >