121. Геометрический и физический смысл производной
Рассмотрим график функции ![]() в декартовой системе координат
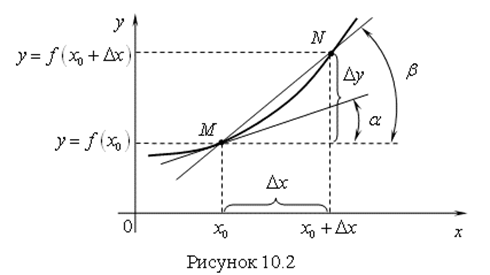
в декартовой системе координат ![]() (рис. 10.2). Возьмем на графике точку
(рис. 10.2). Возьмем на графике точку ![]() и точку
и точку ![]() . Проведем через эти точки прямую
. Проведем через эти точки прямую ![]() . Эта прямая называется Секущей. Ее уравнением будет
. Эта прямая называется Секущей. Ее уравнением будет ![]() , а угловой коэффициент этой прямой равен тангенсу угла наклона секущей:
, а угловой коэффициент этой прямой равен тангенсу угла наклона секущей: 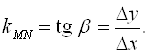
Если ![]() то секущая MN поворачивается вокруг точки
то секущая MN поворачивается вокруг точки ![]() и переходит в касательную с угловым коэффициентом
и переходит в касательную с угловым коэффициентом 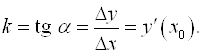
Если ![]() , то секущая MN поворачивается вокруг точки М и в пределе переходит в касательную с угловым коэффициентом
, то секущая MN поворачивается вокруг точки М и в пределе переходит в касательную с угловым коэффициентом 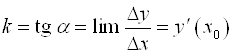 .
.
Угловой коэффициент касательной к графику функции в данной точке равен значению производной функции в этой
точке: ![]() .
.
Геометрический смысл производной состоит в том, что производная равна угловому коэффициенту касательной к графику функции в данной точке.
Значение производной ![]() в точке
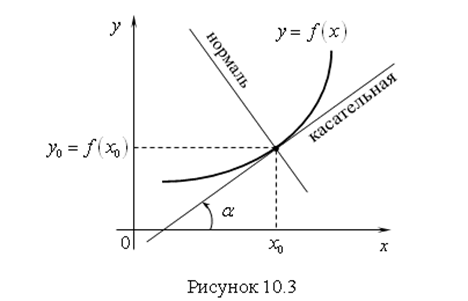
в точке ![]() равно тангенсу угла наклона касательной (рис. 10.3).
равно тангенсу угла наклона касательной (рис. 10.3).
Нормаль – это прямая, перпендикулярная к касательной в точке касания (рис. 10.3).
Уравнение касательной к кривой ![]() в точке
в точке ![]() запишем как уравнение прямой, которая проходит через заданную точку:
запишем как уравнение прямой, которая проходит через заданную точку: ![]() .
.
Уравнение нормали к кривой ![]() в точке
в точке ![]() запишем так:
запишем так: 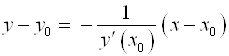 .
.
Пример 1. Напишите уравнение касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() .
.
Решение. 1) Найдем значение функции, если ![]() :
: ![]() .
.
2) Найдем первую производную функции: ![]() .
.
3) Найдем значение производной, если ![]() :
: ![]() .
.
4) Запишем уравнение касательной, которая проходит через данную точку ![]() :
: ![]() или
или ![]() .
.
Ответ. Уравнение касательной: ![]() .
.
Пример 2. Напишите уравнение нормали к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() .
.
Решение. 1) Найдем значение функции, если ![]() :
: ![]() .
.
2) Найдем первую производную функции: ![]() .
.
3) Найдем значение производной, если ![]() :
: ![]() .
.
4) Запишем уравнение нормали, которая проходит через данную точку ![]() :
: 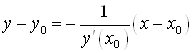 или
или ![]() .
.
Ответ. Уравнение нормали: ![]() .
.
Рассмотрим задачу о свободном падении тела и найдем мгновенную скорость его движения.
Из физики мы знаем, что 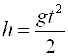 , где H – высота падения, G – ускорение свободного падения, T – время падения.
, где H – высота падения, G – ускорение свободного падения, T – время падения.
За время ![]() тело проходит расстояние
тело проходит расстояние 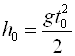 , а за время
, а за время ![]() – расстояние
– расстояние 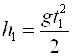 . Приращение аргумента (времени T) будет равно
. Приращение аргумента (времени T) будет равно ![]() , откуда
, откуда ![]() .
.
Приращение функции ![]() будет равно:
будет равно:
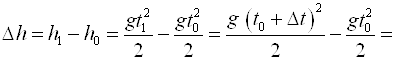
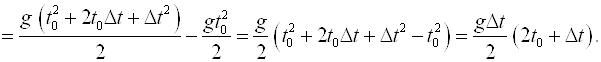
Найдем предел отношения приращения функции ![]() к приращению ее аргумента T , если ΔT Стремится к нулю:
к приращению ее аргумента T , если ΔT Стремится к нулю:
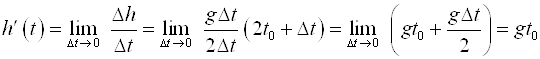 .
.
В левой части равенства мы получили значение производной функции ![]() , а в правой части значение мгновенной скорости тела в момент времени T0.
, а в правой части значение мгновенной скорости тела в момент времени T0.
Физический смысл производной. Производная функции ![]() в точке
в точке ![]() есть мгновенная скорость изменения функции в точке
есть мгновенная скорость изменения функции в точке ![]() , т. е. скорость протекания процесса, который описывается зависимостью
, т. е. скорость протекания процесса, который описывается зависимостью ![]() .
.
Например, если дана функция ![]() , то ее производная будет
, то ее производная будет ![]() , тогда значение производной в точке
, тогда значение производной в точке ![]() будет
будет ![]() , а значение производной в точке
, а значение производной в точке ![]() будет
будет ![]() . Это значит, что в точке
. Это значит, что в точке ![]() функция изменяется в 4 раза быстрее аргумента
функция изменяется в 4 раза быстрее аргумента ![]() , а в точке
, а в точке ![]() изменяется в 6 раз быстрее (т. е. различная скорость изменения функции или протекания процесса). В этом и состоит физический смысл производной.
изменяется в 6 раз быстрее (т. е. различная скорость изменения функции или протекания процесса). В этом и состоит физический смысл производной.
Операция нахождения (взятия) производной функции ![]() называется Дифференцированием функции.
называется Дифференцированием функции.
Ответьте на вопросы
1. Что показывает угловой коэффициент K в уравнении прямой ![]() ?
?
2. Чему равен угловой коэффициент касательной к кривой в точке ![]() ?
?
3. Как найти угловой коэффициент нормали к кривой в точке ![]() ?
?
4. В чем состоит геометрический смысл производной?
5. В чем состоит физический смысл производной?
| < Предыдущая | Следующая > |
|---|