120. Понятие производной

Пусть есть функция, которая определена на отрезке , и точка принадлежит этому интервалу. Возьмем произвольную точку из этого интервала, составим разность и обозначим ее (читаем: "дельта икс"): . Эта разность называется Приращение аргумента функции (рис. 10.1).

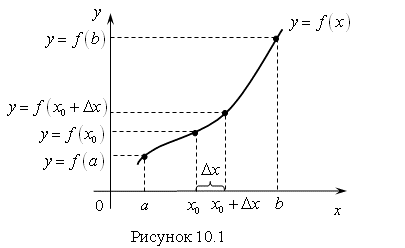
Разность между значением функции в точке и значением функции в точке называется Приращением функции и обозначается (читается: "дельта игрек"):

.

Найдем предел отношения приращения функции к приращению аргумента, если стремится к , а стремится к нулю. Это будет новая функция. Обозначим ее (читаем: "игрек штрих"):

.

Если этот предел существует, то функция Имеет производную в данной точке , или она Дифференцируема в этой точке.

Производная функции есть предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

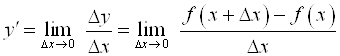
В литературе используют различные обозначения для производных: или – Лагранж, или – Лейбниц, или – Коши.

Производную функции в точке обозначают так:

Ответьте на вопросы

1. Что такое приращение аргумента, приращение функции?

2. Как прочитать выражение ?

3. Что такое производная функции?

< Предыдущая		Следующая >