117. Некоторые способы вычисления пределов

1. Для непрерывных при функций пределы при вычисляют подстановкой значения в выражение функции.

Например, .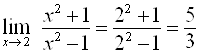

2. Если при знаменатель равен нулю, а числитель не равен нулю, предел функции при не существует. Условно говорят, что он равен бесконечности.

Например, .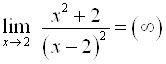

3. Если при и числитель, и знаменатель равны нулю, говорят, что есть Неопределенность Вида и ее надо Раскрыть. Для этого можно:

А) Числитель и знаменатель разложить на множители и сократить на ;

Например, ;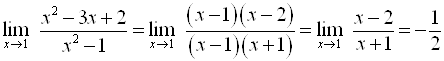

Б) Если под знаком предела есть иррациональные выражения, то надо умножить числитель и знаменатель на выражения, сопряженные иррациональному выражению и после этого найти предел;

Например,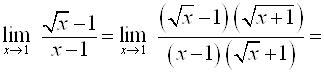

.

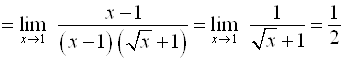В) Если под знаком предела есть тригонометрические функции, надо использовать первый замечательный предел или его следствия.

Например, .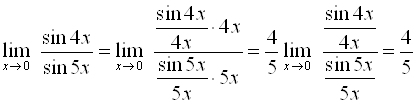

4. Если , то предел отношения двух многочленов равен:

5. Для раскрытия неопределенностей вида () применяют второй замечательный предел или его свойства.

Например,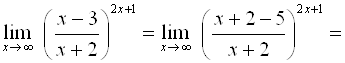

.

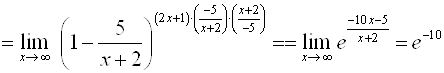< Предыдущая		Следующая >