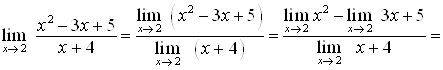115. Предел и непрерывность функции
Построим график функции ![]() (рис. 9.1).
(рис. 9.1).
При приближении переменной ![]() к точке
к точке ![]() переменная
переменная ![]() приближается к точке
приближается к точке ![]() . Говорят, что число 3 является пределом функции
. Говорят, что число 3 является пределом функции ![]() при
при ![]() , стремящемся к единице. Пишут:
, стремящемся к единице. Пишут: ![]() . Читают: "Лимит эф от икс при икс, стремящемся к единице, равен 3".
. Читают: "Лимит эф от икс при икс, стремящемся к единице, равен 3".
Рассмотрим интервал вблизи точки ![]() ограниченный бесконечно малой
ограниченный бесконечно малой ![]() , это будет
, это будет ![]() или
или ![]() . Это же можно записать и в форме
. Это же можно записать и в форме ![]() .
.
Интервал ![]() называют
называют ![]() – окрестностью точки А (
– окрестностью точки А (![]() – "дельта").
– "дельта").
Составим разность ![]() . Модуль этой разности
. Модуль этой разности ![]() меньше числа
меньше числа ![]() ("эпсилон"), если
("эпсилон"), если ![]() .
.
Действительно, ![]() откуда
откуда ![]() . Значит, для любого
. Значит, для любого ![]() можно найти
можно найти ![]() (у нас
(у нас ![]() ) такое, что если
) такое, что если ![]() , то всегда
, то всегда ![]() . На основании этого запишем новое определение предела.
. На основании этого запишем новое определение предела.
Число ![]() называется Пределом функции
называется Пределом функции ![]() при
при ![]() , стремящемся к
, стремящемся к ![]() , если для любого
, если для любого ![]() можно найти такое
можно найти такое ![]() , что из
, что из ![]() следует
следует ![]()
![]() .
.
Если функция ![]() имеет предел, когда Х стремится к А, оставаясь всегда меньше А, то говорят, что она имеет Предел слева, и пишут:
имеет предел, когда Х стремится к А, оставаясь всегда меньше А, то говорят, что она имеет Предел слева, и пишут: ![]() .
.
Если функция ![]() имеет предел, когда
имеет предел, когда ![]() стремится к
стремится к ![]() , оставаясь всегда больше
, оставаясь всегда больше ![]() , то говорят, что она имеет Предел справа, и пишут:
, то говорят, что она имеет Предел справа, и пишут: ![]() .
.
Например, функция 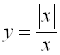 имеет предел слева, равный
имеет предел слева, равный ![]() , и предел справа, равный 1 (рис. 9.2).
, и предел справа, равный 1 (рис. 9.2).
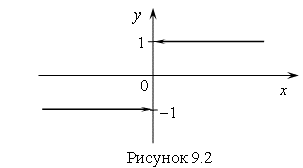
Функция может иметь только один из пределов (слева или справа), или не иметь границ вообще.
Например, функция![]() имеет предел справа
имеет предел справа ![]() , а предел слева
, а предел слева ![]() не существует, так как эта функция не определена для
не существует, так как эта функция не определена для ![]() .
.
Функция может и не иметь вообще пределов в какой-то точке. Для функции 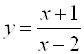 предел
предел 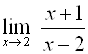 не существует ни справа, ни слева.
не существует ни справа, ни слева.
Для решения задач по вычислению пределов и их применению полезно знать следующие основные теоремы о пределах.
Теорема 1. Если существуют пределы функций ![]() и
и ![]() при
при ![]() , то существует и предел их суммы, равный сумме пределов этих функций:
, то существует и предел их суммы, равный сумме пределов этих функций:
![]() .
.
Теорема 2. Если существуют пределы функций ![]() и
и ![]() при
при ![]() , то существует и предел их произведения, равный произведению пределов этих функций:
, то существует и предел их произведения, равный произведению пределов этих функций:
![]() .
.
Следствие. Постоянный множитель можно вынести за знак предела:
![]() .
.
Теорема 3. Если существуют пределы функций ![]() и
и ![]() при
при ![]() , и
, и ![]() , то существует и предел их отношения, равный отношению пределов этих функций:
, то существует и предел их отношения, равный отношению пределов этих функций:
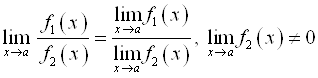 .
.
Для нахождения пределов функций также как и для последовательностей, применяют теоремы о пределах суммы, произведения, частного, степени функций.
Рассмотрим решение некоторых примеров.
Пример 22. Найдите предел ![]() .
.
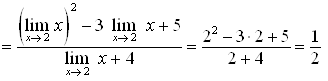 .
.
В этом примере, чтобы вычислить предел функции, можно подставить в нее ![]() , так как числитель и знаменатель стремятся к конечным пределам и предел знаменателя не равен нулю.
, так как числитель и знаменатель стремятся к конечным пределам и предел знаменателя не равен нулю.
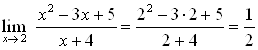 .
.
Ответ. 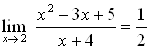 .
.
Пример 23. Найдите предел ![]() .
.
Решение.  .
.
Ответ. ![]() .
.
Пример 24. Найдите предел 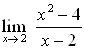 .
.
Решение. В данном случае числитель и знаменатель стремятся к нулю при ![]() . Разложим числитель на множители
. Разложим числитель на множители ![]() и сократим числитель и знаменатель на
и сократим числитель и знаменатель на ![]() :
:
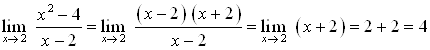 .
.
Ответ. 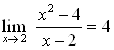 .
.
Геометрически непрерывность функции в точке означает, что ее график можно провести через эту точку, не отрывая карандаш от плоскости чертежа.
Пример 25. Постройте графики следующих четырех функций и рассмотрите их поведение в окрестности точки ![]() :
:
1) ![]() , 2)
, 2) 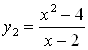 , 3)
, 3)  , 4)
, 4) ![]() .
.
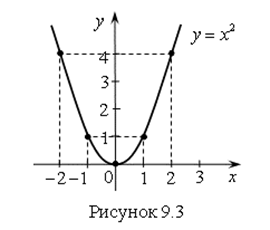
Решение. 1) Найдем предел функции ![]() (рис. 9.3).
(рис. 9.3).
Для переменных ![]() предел слева равен
предел слева равен ![]() .
.
Для переменных ![]() предел справа равен
предел справа равен ![]() .
.
Предел функции ![]() в точке
в точке ![]() равен
равен ![]() .
.
Значение функции ![]() в точке
в точке ![]() равно
равно ![]() .
.
![]() .
.
Предел функции слева равен пределу функции справа и равен пределу функции в точке.
Вывод: Предел функции ![]() при
при ![]() существует и равен значению функции в точке
существует и равен значению функции в точке ![]() .
.
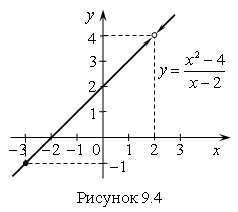
2) Найдем предел функции ![]() (рис. 94).
(рис. 94).
Для ![]() предел функции слева равен
предел функции слева равен ![]() .
.
Для ![]() предел функции справа равен
предел функции справа равен  .
.
Предел функции 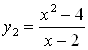 в точке
в точке ![]() равен
равен 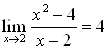 .
.
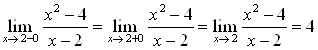 .
.
Предел функции слева равен пределу функции справа и равен пределу функции в точке, но в точке ![]() знаменатель функции равен нулю и функция неопределена.
знаменатель функции равен нулю и функция неопределена.
Вывод: Предел функции 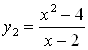 существует и равен 4, но не равен значению функции в точке
существует и равен 4, но не равен значению функции в точке ![]() .
.
3) Найдем предел функции  (рис. 9.5).
(рис. 9.5).
Для ![]() предел функции слева равен
предел функции слева равен 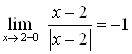 .
.
Для ![]() предел функции справа равен
предел функции справа равен 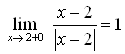 .
.
При ![]() функция неопределенна (не существует).
функция неопределенна (не существует).
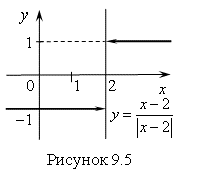
Вывод: Предел слева функции  при
при ![]() Не равен пределу справа и функция
Не равен пределу справа и функция ![]() в точке
в точке ![]() не существует.
не существует.
4) Найдем предел функции ![]() (рис. 9.6).
(рис. 9.6).
Для ![]() предел функции слева равен
предел функции слева равен ![]() .
.
Для ![]() предел функции справа равен
предел функции справа равен ![]() .
.
При ![]() функция неопределенна (не существует).
функция неопределенна (не существует).
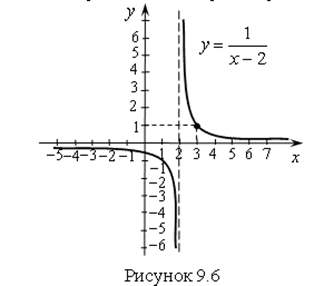
Вывод: Предел функции, а также значение функции в точке ![]() не существует.
не существует.
Ответ. Из рассмотренных примеров видно, что в точке ![]() непрерывна только функция
непрерывна только функция ![]() .
.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если:
, если:
1) она определена в окрестности этой точки;
2) имеет предел, когда ![]() стремится к
стремится к ![]() произвольно:
произвольно:
![]() ;
;
3) предел функции ![]() при
при ![]() равен значению функции в этой точке:
равен значению функции в этой точке:
![]() .
.
Если функция не является непрерывной в точке ![]() , эту точку называют Точкой разрыва функции.
, эту точку называют Точкой разрыва функции.
В рассмотренных примерах ![]() является точкой разрыва функций
является точкой разрыва функций ![]()
![]() и
и ![]() . Разрывы такого типа, как у функции
. Разрывы такого типа, как у функции ![]() Устранимы.
Устранимы.
Устранить разрыв, значит, сделать функцию непрерывной. Для ![]() это можно сделать, если задать ее следующим образом:
это можно сделать, если задать ее следующим образом: 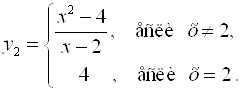 Такое задание называют Доопределением функции.
Такое задание называют Доопределением функции.
Устранить разрывы функций ![]() и
и ![]() нельзя. Такие неустранимые разрывы называются Скачками. Скачки бывают конечными (как у функции
нельзя. Такие неустранимые разрывы называются Скачками. Скачки бывают конечными (как у функции ![]() ) и бесконечными (как у функции
) и бесконечными (как у функции ![]() ).
).
Если использовать понятия приращения аргумента ![]() и приращения функции
и приращения функции ![]() , то можно дать еще одно определение непрерывности.
, то можно дать еще одно определение непрерывности.
Функция ![]() называется Непрерывной в точке
называется Непрерывной в точке ![]() , если она определена в окрестности этой точки, и если приращение аргумента
, если она определена в окрестности этой точки, и если приращение аргумента ![]() стремится к нулю, то и приращение функции
стремится к нулю, то и приращение функции ![]() также стремится к нулю.
также стремится к нулю.
![]() или
или ![]() ,
,
Откуда ![]() .
.
Функция ![]() называется Непрерывной в точке
называется Непрерывной в точке ![]() , если она определена в окрестности этой точки и предел функции при
, если она определена в окрестности этой точки и предел функции при ![]() равен значению функции в этой точке:
равен значению функции в этой точке:
![]() .
.
Функция, непрерывная во всех точках интервала, называется Непрерывной в этом интервале.
Все элементарные функции непрерывны в области их определения.
Пример 26. Проверьте непрерывность функции ![]() в точках
в точках ![]() и
и ![]() .
.
Решение.
I. Проверим непрерывность функции в точке ![]() .
.
1. Функция ![]() определена в точке
определена в точке ![]() и ее значение в этой точке равно:
и ее значение в этой точке равно: ![]() .
.
2. Найдем пределы функции в окрестности точки ![]() :
:
А) слева ![]() ;
;
Б) справа ![]() ;
;
В) ![]() .
.
3. Предел функции в точке ![]() равен значению функции в этой точке. Функция непрерывна в этой точке.
равен значению функции в этой точке. Функция непрерывна в этой точке.
II. Проверим непрерывность функции ![]() в точке
в точке ![]() .
.
1. В точке ![]() функция неопределена, так как знаменатель функции при
функция неопределена, так как знаменатель функции при ![]() обращается в ноль.
обращается в ноль.
2. Найдем пределы функции в окрестности точки ![]() :
:
А) слева 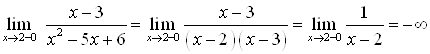 ;
;
Б) справа ![]() ;
;
В) предел функции слева не равен ее пределу справа. В точке ![]() функция
функция ![]() имеет неустранимый разрыв. Точка
имеет неустранимый разрыв. Точка ![]() есть точка разрыва функции.
есть точка разрыва функции.
Ответ. В точке ![]() функция непрерывна, а в точке
функция непрерывна, а в точке ![]() функция имеет неустранимый разрыв.
функция имеет неустранимый разрыв.
| < Предыдущая | Следующая > |
|---|