114. Предел числовой последовательности

Рассмотрим последовательность, которая задана формулой ее -го члена .

Например, 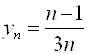– это бесконечная числовая последовательность, где N Î N. Члены этой последовательности при возрастании номера N "стремятся" к . Это видно, если записать N-й член последовательности в виде 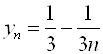. При возрастании номера второе слагаемое "стремится к нулю". Записывают это следующим образом: .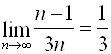

Читают так: "Предел отношения "" к "", при стремящемся к бесконечности, равен ". Считают, что предел этой последовательности равен .

А теперь поставим такой вопрос, каким должно быть , чтобы модуль разности 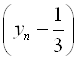был меньше 0,001?

Так как 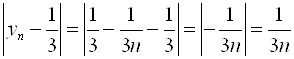, то вопрос сводится к тому, чтобы найти, при каких выполняется неравенство 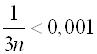. Или , откуда 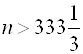. Получаем, что неравенство 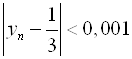выполняется для любого . Если вместо 0,001 мы возьмем 0,000001, то таким же подсчетом мы установим, что 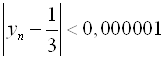при любом .

Для любого произвольного положительного числа (эпсилон) неравенство 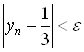будет выполняться при 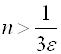. Так как нас интересуют только целые N, то данное неравенство выполняется при всех N > N, где N – целая часть числа .

Число называется Пределом последовательности , если для любого положительного числа найдется такое натуральное число , что при всех выполняется неравенство: .

Говорят: "Предел последовательности равен " и пишут: .

О последовательности, имеющей предел, говорят, что она Сходится. Выясним геометрический смысл понятия предела последовательности.

Неравенство равносильно двойному неравенству или . Это двойное неравенство показывает, что все члены последовательности (Хn), сходящейся к числу А, с номерами , попадают в интервал , который называется ‑окрестностью точки .

При рассмотрении числовых последовательностей возможны только два случая.

1. У последовательности есть предел, и он единственный. Такую последовательность называют Сходящейся.

2. У последовательности нет предела. Такую последователь-ность называют Расходящейся.

Сформулируем три теоремы, которые удобно использовать при вычислении пределов.

Теорема 1. Если последовательности (Хn) и (Yn) сходятся, то

.

Теорема 2. Если последовательности (Хn) и (Yn) сходятся, то

.

Следствие теоремы 2. Постоянный множитель можно выносить за знак предела:

Теорема 3. Если последовательности (Хn) и (Yn) сходятся, и предел последовательности (Yn) отличен от нуля (), то

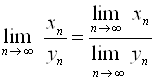
Последовательность называется Бесконечно малой последовательностью или просто бесконечно малой, если ее предел равен нулю:

Например, последовательность 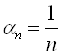является бесконечно малой, так как 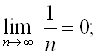последовательность , (Q < 1), является бесконечно малой, так как .

Для бесконечно малых последовательностей можно записать следующие теоремы.

Теорема 1. Сумма двух бесконечно малых последовательностей является бесконечно малой последовательностью.

Теорема 2. Произведение ограниченной последовательности на бесконечно малую последовательность является бесконечно малой последовательностью.

Теорема 3. Произведение двух бесконечно малых последователь-ностей является бесконечно малой последовательностью

Пределы последовательностей можно находить, используя следующее определение предела.

Если последовательность (Xn) можно записать в виде суммы

,

Где С – некоторое постоянное число, а – бесконечно малая,

То С является пределом последовательности (Xn):

Рассмотрим решение примеров с использованием теорем о пределах.

Пример 18. Вычислите предел .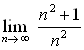

Решение. .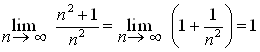

Здесь – бесконечно малая величина, так как .

Ответ. .

Для приведения общего члена последовательности к виду применяют теоремы о пределе суммы, произведения и частного пределов.

Пример 19. Вычислите предел .

Решение. .

Ответ. .

Пример 20. Вычислите предел .

Решение. Применить теорему о пределе суммы нельзя, так как неясно, к чему стремится сумма пределов слагаемых. Чтобы найти предел, вынесем за скобки :

.

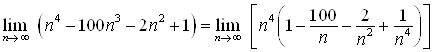К последнему пределу можно применить теорему о пределе произведения:

.

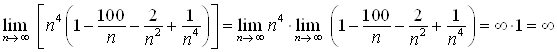Ответ. .

Пример 21. Найдите предел .

Решение. Умножим и разделим выражение, стоящее под знаком предела, на сопряженное ему выражение . Тогда

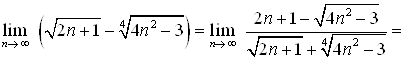
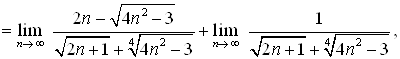
Так как , то

.

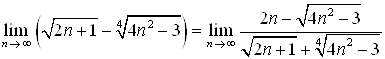Найдем предел числителя:

.

Найдем предел знаменателя:

.

Так как предел знаменателя равен бесконечности, то последовательность бесконечно мала, и .

Ответ. .

< Предыдущая		Следующая >