112. Совместное применение арифметической и геометрической прогрессии
Пример 15. Четыре числа составляют геометрическую прогрессию. Если из первого числа вычесть 11, из второго 1, из третьего 3, а из четвертого 9, то получится арифметическая прогрессия. Найдите эти числа.
Решение. Пусть ![]() ;
; ![]() ;
; ![]() ;
; ![]() – члены геометрической прогрессии. Пусть
– члены геометрической прогрессии. Пусть ![]() ;
; ![]() ;
; ![]() ;
; ![]() – соответствующие члены арифметической прогрессии. Тогда
– соответствующие члены арифметической прогрессии. Тогда ![]() ;
; ![]() ;
; ![]() и
и ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Используем свойство арифметической прогрессии:
![]() ;
; ![]() .
.
Используя полученные выше равенства, запишем систему двух уравнений с двумя неизвестными ![]() и
и ![]() :
:
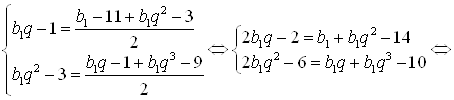
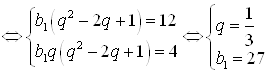 .
.
Запишем геометрическую прогрессию: ![]() ;
; ![]() ;
; ![]() .
.
Ответ. 27; 9; 3; 1.
Пример 16. Найдите четыре числа, из которых первые три составляют геометрическую прогрессию, а последние три – арифметическую, если сумма крайних чисел равна 35, а сумма средних равна 30.
Решение. Пусть числа, которые нужно найти, – это: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда
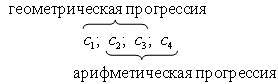
Перепишем условие задачи в виде: 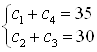 .
.
Выразим через ![]() и
и ![]() все заданные члены:
все заданные члены:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Запишем систему уравнений из условия ![]() и свойства арифметической прогрессии
и свойства арифметической прогрессии ![]() :
:
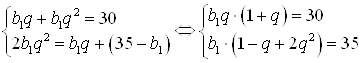 .
.
Решим систему способом деления: 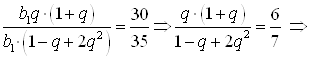
![]()
![]() и
и ![]() .
.
Получим два решения:
1) ![]() ;
; 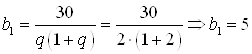 ;
;
2) ![]() ;
; 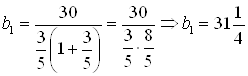 .
.
Ответ. 1) ![]() ;
; ![]() ;
; ![]() ;
; ![]() . 2)
. 2) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Пример 17. Три числа составляют возрастающую геометрическую прогрессию. Если ко второму числу прибавить 2, то полученные числа составят арифметическую прогрессию, а если затем к третьему числу прибавить 9, то прогрессия опять станет геометрической. Найдите эти числа.
Решение. Запишем три прогрессии по условию задачи:
1) :: ![]() ;
; ![]() ;
; ![]() ; 2) :
; 2) : ![]() ;
; ![]() ;
; ![]() ; 3) ::
; 3) :: ![]() ;
; ![]() ;
; ![]() .
.
Для последних двух прогрессий применим их свойства и запишем систему уравнений: 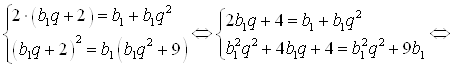
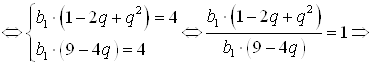
![]() и
и ![]() .
.
По условию задачи геометрическая прогрессия возрастающая, следовательно, ![]() . Найдем первый член прогрессии:
. Найдем первый член прогрессии:  . Значит
. Значит ![]() ,
, ![]() .
.
Ответ. :: 4; 8; 16.
| < Предыдущая | Следующая > |
|---|