111. Геометрическая прогрессия
Геометрическая прогрессия – это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число 
, где – знаменатель прогрессии: 
(
).
Общий вид геометрической прогрессии:
:: 
; 
; 
; ...; 
; ...
Геометрическая прогрессия является возрастающей при 
и убывающей при 
.
Например, :: 2; 6; 18; 54; ...; 
– возрастающая прогрессия; :: 250; 50; 10; ...; 
– убывающая прогрессия.
Если заданы первый член и знаменатель , то 
-й член геометрической прогрессии определяют по формуле:
.
Сумму первых членов Геометрической прогрессии находят по формуле: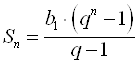 
.
Свойства геометрической прогрессии.
1. Квадрат каждого среднего члена прогрессии равен произведению равноотстоящих от него членов:
; (
).
2. В конечной геометрической прогрессии произведения двух членов, равноотстоящих от ее концов, равны между собой и равны произведению крайних членов:
:: ; ; ; ...; 
; 
; ...; 
; 
; 
.
Пример 7. Найдите первый и последний члены геометрической прогрессии, которая состоит из четырех членов, если 
и 
.
Решение. Подставим исходные данные в формулу:
.
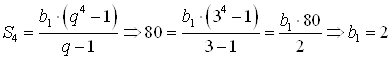Найдем 
по формуле 
и получим: 
.
Ответ. 
и 
.
Пример 8. В геометрической прогрессии (
): 
. Найдите сумму восьми первых членов прогрессии 
.
Решение. 
; 
; 
, тогда запишем исходную систему так: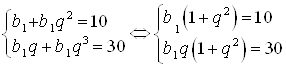 
.
Разделим почленно второе уравнение на первое. Получим:
.
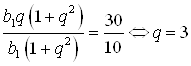Найдем 
из первого уравнения системы: 
.
По формуле для суммы найдем: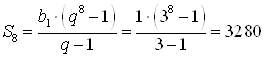 
.
Ответ. 
.
Пример 9. Шесть чисел составляют геометрическую прогрессию. Сумма первых трех чисел равна 168, а сумма последних трех чисел равна 21. Найдите эти числа.
Решение. Из условия задачи составим систему уравнений:
Найдем 
, для этого разделим первое уравнение на второе: 
.
Найдем из первого уравнения: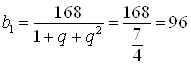 
.
Ответ. 96; 48; 24; 12; 6; 3.
Пример 10. Найдите сумму 
, 
.
Решение. По условию задания можно сделать вывод о том, что: 
– это геометрическая прогрессия. Найдем первый член прогрессии, знаменатель и общее количество ее членов: 
; 
; 
. Тогда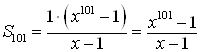 
.
Ответ. 
.
Бесконечно убывающая геометрическая прогрессия – это такая бесконечная геометрическая прогрессия (), у которой знаменатель .
Сумму бесконечно убывающей геометрической прогрессии находят по формуле:
.
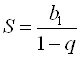Пример 11. Запишите периодическую дробь 0,4545...=0,(45) как обыкновенную.
Решение. Запишем периодическую дробь в виде бесконечной суммы обыкновенных дробей: 
.
Слагаемые представляют собой бесконечно убывающую геометрическую прогрессию со знаменателем 
и первым членом 
, а полученная сумма – это сумма этой прогрессии.
Используя формулу суммы бесконечно убывающей геометрической прогрессии, получим: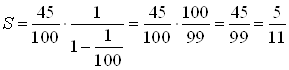 
.
Ответ. 
.
Пример 12. Найдите бесконечно убывающую геометрическую прогрессию, если , а сумма 
.
Решение. Используя формулу суммы бесконечно убывающей геометрической прогрессии найдем:
.
Ответ. :: 
; 
; 
; ...
Пример 13. Найдите бесконечно убывающую геометрическую прогрессию, если ее сумма равна 
, а сумма ее первых четырех членов равна 
.
Решение. Из условия задачи запишем систему:
.
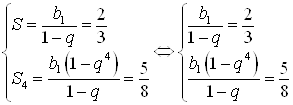Подставим правую часть первого уравнения во второе уравнение:
И 
.
Тогда найдем два значения :
1) 
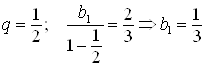; 2) 
.
Ответ. 1) :: 
; 
; 
; 
; ...; 2) :: ; 
; 
; 
; ... .
Пример 14. Сумма бесконечно убывающей геометрической прогрессии 
, а сумма квадратов всех ее членов 
. Найти четвертый член прогрессии.
Решение. Найдем знаменатель прогрессии, которая состоит из квадратов членов: 
; 
; 
; ...; 
; ... : 
.
Тогда составим систему уравнений: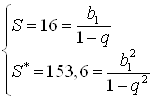 
.
Возведем первое уравнение в квадрат: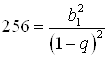 
.
Разделим второе уравнение системы на первое:
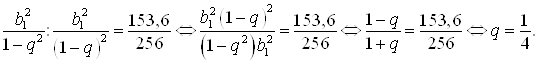
Тогда 
; 
.
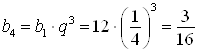Ответ. 
.
| < Предыдущая | Следующая > |
|---|
