110. Арифметическая прогрессия

Арифметическая прогрессия – это числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и постоянного числа , где – это разность прогрессии: , .

Общий вид арифметической прогрессии:

; ; ; ...; ; ... .

Очевидно, что прогрессия является возрастающей, если , и убывающей, если .

Например, 2; 5; 8; 11; ... () – возрастающая прогрессия;

12; 10; 8; 6; ... () – убывающая прогрессия.

Если заданы первый член и разность , то -Й член прогрессии (любой член) Определяют по формуле:

.

Сумма первых членов Арифметической прогрессии вычисляется по формулам:

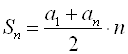или ,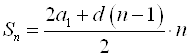

Где – количество членов прогрессии.

Свойства арифметической прогрессии.

1. Каждый средний член равен полусумме равноотстоящих от него членов: , ().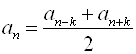

2. В конечной арифметической прогрессии суммы двух членов, равноотстоящих от ее концов, равны между собой и равны сумме крайних членов:

; ; ; ...; ; ... ; ; ...; ; ; .

Пример 1. Найдите семнадцатый член арифметической прогрессии:
3; 7; 11: 15; ... .

Решение. Найдем разность прогрессии: . Тогда .

Ответ. .

Пример 2. Разность арифметической прогрессии равна 3, а сумма первых ее шести членов равна 57. Найдите , .

Решение. ; . Тогда

; .

Ответ. ; .

Пример 3. Третий член арифметической прогрессии равен 6, а седьмой 14. Сколько членов нужно взять, чтобы их сумма была равна 110?

Решение. ; . Запишем и , используя формулу и вычислим и :

; .

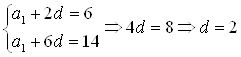Подставим значения и в формулу и получим уравнение для вычисления :

; . Значение – не будет решением, так как .

Ответ. .

Пример 4. Найдите арифметическую прогрессию, если сумма ее первых членов .

Решение. По условию: ; .

можно найти также как сумму первого и второго членов арифметической прогрессии, тогда:.

Отсюда .

Ответ. , или .

Пример 5. Найдите арифметическую прогрессию, если сумма первых трех ее членов равна 15, сумма трех последних членов равна 39, а сумма всех членов равна 63.

Решение. 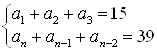(из условия).

Сложим равенства: . По второму свойству арифметической прогрессии суммы в скобках равны между собой: . Найдем число членов прогрессии, используя формулу: . Подставим значение в исходную систему, получим:

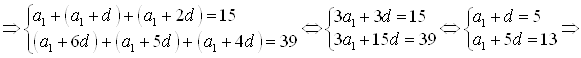
и . Запишем прогрессию, зная и .

Ответ. 3; 5; 7; 9; 11; 13; 15.

Пример 6. Между числами 1 и 25 напишите пять чисел, которые с данными числами составляют арифметическую прогрессию.

Решение. ; ; . Но, .

Ответ. 1; 5; 9; 13; 17; 21; 25; ...

< Предыдущая		Следующая >