106. Тригонометрические неравенства

При решении неравенств с тригонометрическими функциями используются периодичность этих функций и их монотонность на соответствующих интервалах.

Рассмотрим решение простейших тригонометрических неравенств.

1. , , , , .

Множество решений этих неравенств найдем с помощью графика функции . Функция имеет наименьший положительный период . Поэтому такие неравенства удобно решать сначала на интервале .

Для решения таких неравенств, как правило, используют следующую последовательность действий:

- строим график функции ;

- проводим прямую ;

- находим точки пересечения этой прямой с частью графика (на отрезке длиной в );

- проецируем эти точки на ось ;

- получаем множество решений данного неравенства на рассматриваемом интервале;

- прибавим числа вида к каждому из найденных решений (на отрезке длиной ). Получим множество всех решений исходного неравенства.

Пример 39. Решите неравенство .

Решение. Построим график функции (рис. 8.14).

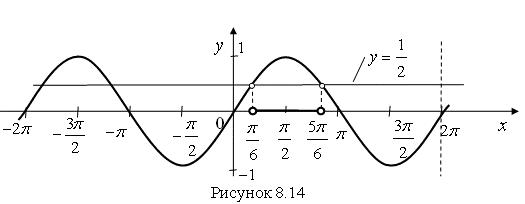
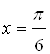Выберем отрезок и проведем прямую . Найдем точки пересечения этой прямой с синусоидой. Спроецируем эти точки на ось , получим точки и 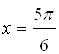. На графике видно, что при 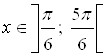, 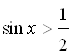. Поэтому, точки интервала 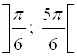являются множеством решений неравенства 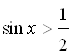на отрезке .

Множество всех решений неравенства – совокупность интервалов:

.

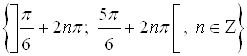Ответ. .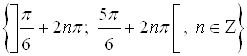

2. , , .

Множество решений этих неравенства найдем с помощью графика функции . Функция имеет наименьший положительный период . Поэтому такие неравенства удобно решать сначала на каком-либо интервале длиной в , а именно на интервале ("впадина" на графике ).

Далее решение исходных неравенств осуществляется по аналогии с тем, как решались неравенства , , , . Рассмотрим это на примерах.

Пример 40. Решите неравенство .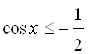

Решение. Построим график функции (рис. 8.15)

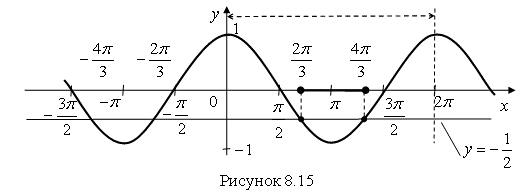
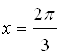Выберем отрезок и проведем прямую . Найдем точки пере-сечения этой прямой с косинусоидой. Спроецируем эти точки на ось , получим точки и 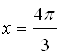. Поэтому точки интервала 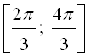являются множеством решений неравенства 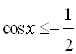на отрезке .

Множество всех решений неравенства – совокупность интервалов: .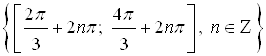

Ответ. .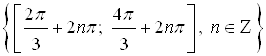

2 а. , , .

Множество решений этих неравенств найдем также с помощью графика функции . Такие неравенства также удобно решать на интервале длиной в , а именно на интервале ("холмик" на графике ). Далее решают аналогично неравенствам и . Рассмотрим это на примере.

Пример 41. Решить неравенство .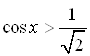

Решение. Постоим график функции (рис. 8.16).

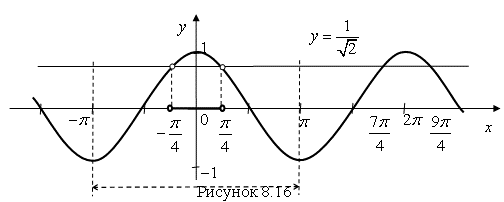
Выберем отрезок и проведем прямую .

Найдем точки пересечения этой прямой с косинусоидой.

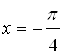Спроецируем эти точки на ось , получим точки и 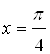. Значит, точки интервала 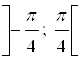являются множеством решений неравенства 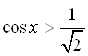на отрезке .

Множество всех решений неравенства – совокупность интервалов .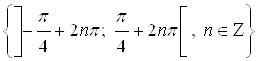

Ответ. .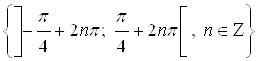

Пример 42. Решите неравенство .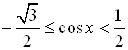

Решение. Рассмотрим график функции на отрезке (рис. 8.17)

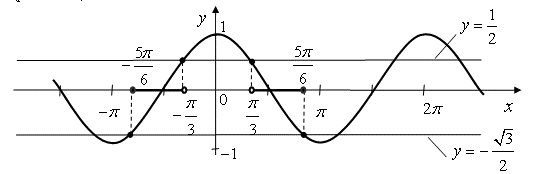
Рисунок 8.17

Рассмотрим части косинусоиды, которые лежат между прямым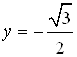и и . Тогда, на отрезке множеством решений неравенства будет объединение интервалов: 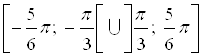. Следовательно, множество всех решений данного неравенства – это совокупность множеств:

.

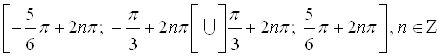Ответ.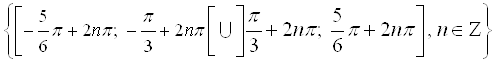

3. , , , .

Множество решений этих неравенств найдем с помощью графика функции . Функция имеет наименьший положительный период . Такие неравенства удобно сначала решать на интервале 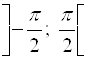. Далее решают аналогично предыдущим неравенствам.

Прибавляя числа вида к найденным решениям на интервале 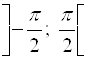, получим все решения неравенств , , , .

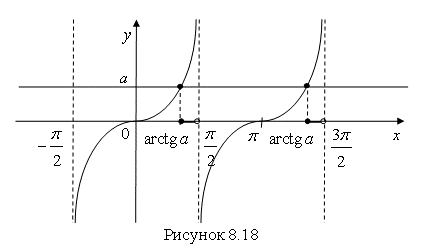
Из графика (рис. 8.18) следует, что множество всех решений неравенства – это совокупность интервалов .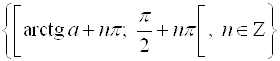

Рассмотрим решения неравенств , , , на примерах.

Пример 43. Решить неравенство .

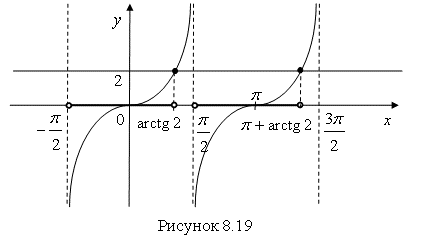
Решение. Построим график функции (рис. 8.19).

Проведем прямую . Найдем точки пересечения этой прямой с тангенсоидой. Спроецируем эти точки на ось , получим точки и . Поэтому точки интервала 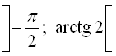являются множеством решений неравенства на интервале 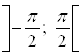. Множество всех решений неравенства – это совокупность интервалов .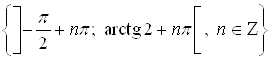

Ответ. .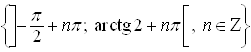

Пример 44. Решите неравенство .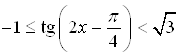

Решение. Сделаем замену . Получим неравенство: .

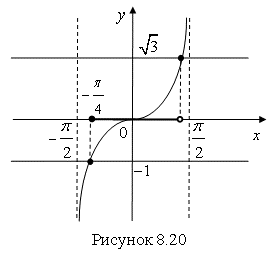
Рассмотрим график функции на интервале 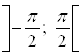и найдем множество решений данного неравенства на этом интервале (рис. 8.20). Множество решений неравенства 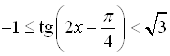на интервале 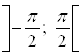– это интервал .

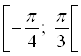Тогда, все решения исходного неравенства будут такими:

.

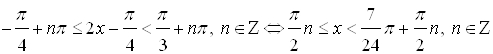Ответ. .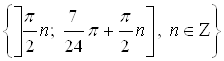

4. , , , .

Множество решений этих неравенств найдем с помощью графика функции . Функция имеет наименьший положительный период . Такие неравенства удобно сначала решать на интервале . Далее решают аналогично предыдущим неравенствам.

Прибавляя числа вида к найденным решениям на интервале , получим все решения неравенств , , , .

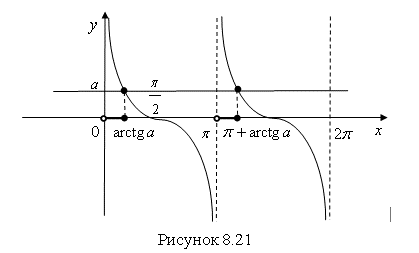
Из графика (рис. 8.21) следует, что множество всех решений неравенства – это совокупность интервалов .

Рассмотрим решение неравенств вида , , , на примерах.

Пример 45. Решите неравенство .

Решение. Построим график функции (рис. 8.22).

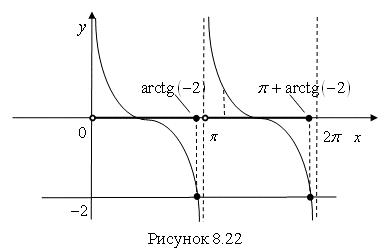
Проведем прямую . Найдем точки пересечения этой прямой с котангенсоидой. Спроецируем эти точки на ось , получим точки и . Поэтому точки интервала являются множеством решений неравенства на интервале .

Множество всех решений неравенства – это совокупность интервалов:

.

Ответ. .

Пример 46. Решите неравенство .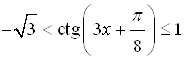

Решение. Сделаем замену: .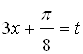

Рассмотрим неравенство (рис. 8.23).

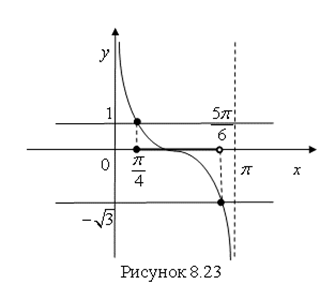
На интервале множество решений данного неравенства – это интервал 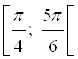. Множество решений данного неравенства – это совокупность промежутков 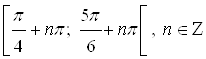. Тогда все решения исходного неравенства будут такими:

.

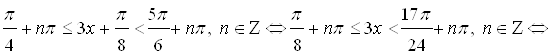
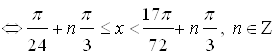Ответ. .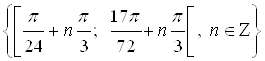

Пример 47. Решите неравенство .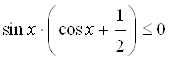

Решение. Данное неравенство эквивалентно совокупности систем неравенств:

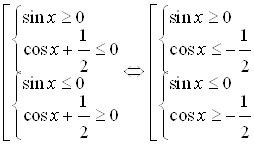
Рассмотрим решение совокупности этих систем, используя графики функций и на отрезке (рис. 8.24).

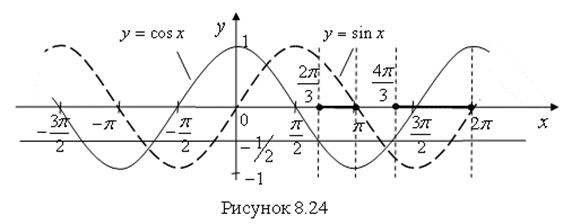
На отрезке решение данного неравенства – множество . Так, множество всех решений данного неравенства – это совокупность множеств

.

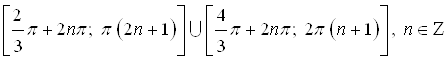Ответ. .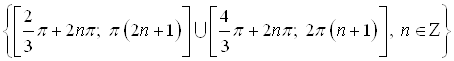

Пример 48. Решите неравенство .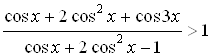

Решение. Найдем область определения данного неравенства:

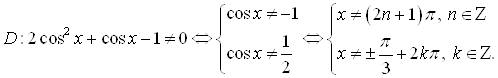
Так, .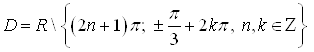

Учитывая, что , запишем данное неравенство в виде: .

Сделаем замену , . Получим систему уравнений:

.

Возвращаемся к неизвестной и учитываем, что при , тогда получим неравенство:

.

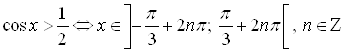Ответ. .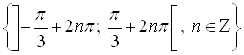

Пример 49. Решите неравенство .

Решение. Умножим обе части исходного неравенства на 2 и используем формулу . Получим:

.

Ответ. .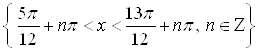

Пример 50. Решите неравенство .

Решение. По определению модуля можно записать, что: и , значит можно возвести обе части исходного неравенства в квадрат. Получим:

.

Ответ. .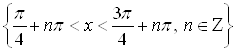

< Предыдущая		Следующая >