105. Системы тригонометрических уравнений
Системы тригонометрических уравнений решают теми же методами, которые используются для решения алгебраических систем: метод подстановки, метод алгебраического сложения, метод замены переменных и другие.
Пример 36. Решите систему уравнений 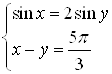 .
.
Решение. Найдем ОДЗ: ![]() .
.
Выразим ![]() из второго уравнения и подставим его в первое:
из второго уравнения и подставим его в первое:
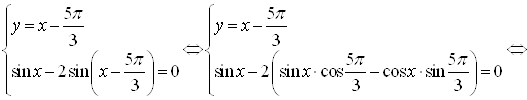
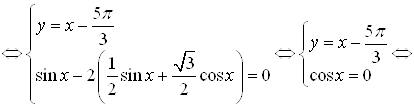

Ответ. 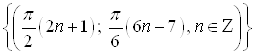 .
.
Пример 37. Решите систему уравнений 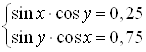 .
.
Решение. Область определения системы уравнений ![]() . Сложим и вычтем уравнения системы:
. Сложим и вычтем уравнения системы: 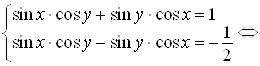
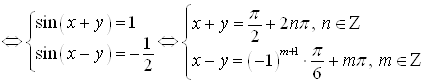 .
.
Обратите внимание, что нельзя в обоих уравнениях записать решения, используя только ![]() , например, если:
, например, если: 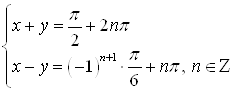 , то это может привести к потере решений.
, то это может привести к потере решений.
Рассмотрим для второго уравнения сначала ![]() , а затем
, а затем ![]() :
:


Ответ. 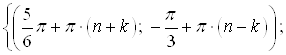
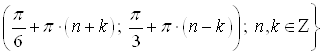 .
.
Пример 38. Решите систему уравнений 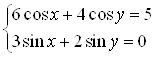 .
.
Решение. Область определения системы уравнений ![]() .
.
Запишем систему уравнений в виде: 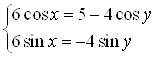 .
.
Возведем оба уравнения в квадрат и сложим их:
![]() .
.
Учитывая, что ![]() , из первого уравнения системы находим:
, из первого уравнения системы находим: ![]() . Итак, получаем четыре множества решений, а именно:
. Итак, получаем четыре множества решений, а именно:
А) 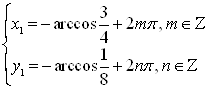 ; б)
; б) 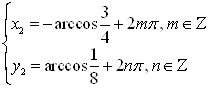 ;
;
В) 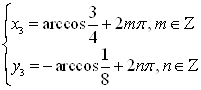 ; г)
; г) 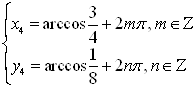 .
.
Так как мы возводили уравнения системы в квадрат, то это могло привести к посторонним решениям. Поэтому полученные решения нужно проверить, подставив их в исходную систему. После проверки определяем, что решения ![]() и
и ![]() – посторонние, а
– посторонние, а ![]() и
и ![]() – это множество решений исходной системы.
– это множество решений исходной системы.
Ответ. 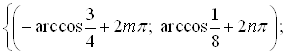
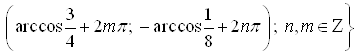 .
.
| < Предыдущая | Следующая > |
|---|