103. Основные методы решения тригонометрических уравнений
Рассмотрим основные методы решения тригонометрических уравнений. Эти уравнения сводятся к простейшим тригоно-метрическим уравнениям, решение которых мы уже рассмотрели.
1. Метод приведения к одной функции
При решении уравнений часто используется основное тригонометрическое тождество ![]() , а также замена переменных.
, а также замена переменных.
Пример 18. Решите уравнение ![]() .
.
Решение. Заменим ![]() на
на ![]() , получим:
, получим:
![]() .
.
Сделаем замену ![]() , получим квадратное уравнение
, получим квадратное уравнение ![]() . Найдем решения:
. Найдем решения:
А) ![]() или
или ![]() ;
;
Б) ![]() или
или ![]() .
.
Ответ. 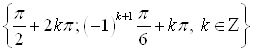 .
.
2. Решение уравнений, однородных относительно ![]() и
и ![]() , а также приводимых к однородным
, а также приводимых к однородным
Однородное тригонометрическое уравнение относительно ![]() и
и ![]() – это такое уравнение, каждый член которого имеет одинаковую степень
– это такое уравнение, каждый член которого имеет одинаковую степень ![]() и
и ![]() , а правая часть уравнения равна нулю.
, а правая часть уравнения равна нулю.
Так, ![]() – это однородное уравнение
– это однородное уравнение ![]() -й степени.
-й степени.
При решении однородных уравнений ![]() -й степени использу-ется деление каждого члена уравнения на
-й степени использу-ется деление каждого члена уравнения на ![]() . При этом исходное уравнение сводится к уравнению относительно
. При этом исходное уравнение сводится к уравнению относительно ![]() . Необходимо проверять, не приведет ли такое деление к потере решений: 1) если
. Необходимо проверять, не приведет ли такое деление к потере решений: 1) если ![]() , то потери решений не будет; 2) если
, то потери решений не будет; 2) если ![]() , то такое деление приведет к потере корней. Следовательно, в ответ нужно включить и решения уравнения
, то такое деление приведет к потере корней. Следовательно, в ответ нужно включить и решения уравнения ![]() , т. е.
, т. е. ![]() ,
, ![]() .
.
Пример 19. Решите уравнение ![]() .
.
Решение. Разделим обе части исходного однородного уравнения первой степени на ![]() , получим:
, получим:
![]() .
.
Ответ. ![]() .
.
Пример 20. Решите уравнение ![]() .
.
Решение. Разделим обе части исходного однородного уравнения второй степени на ![]() . Получим квадратное уравнение относительно
. Получим квадратное уравнение относительно ![]() :
: ![]() . Найдем решения этого уравнения относительно
. Найдем решения этого уравнения относительно ![]() :
:
А) ![]() ;
;
Б) ![]() ,
, ![]()
Ответ. ![]() .
.
Пример 21. Решите уравнение ![]() .
.
Решение. Исходное уравнение не является однородным, но его можно привести к однородному при помощи замены ![]() . Получим:
. Получим:
![]()
![]() .
.
Разделим все члены уравнения на ![]() . Получим:
. Получим:
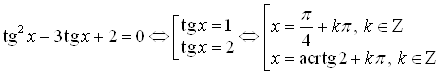 .
.
Ответ. ![]() .
.
3. Метод разложения на множители
Использование этого метода основано на том, что уравнение ![]() равносильно совокупности уравнений
равносильно совокупности уравнений 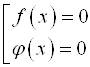 в области определения уравнения
в области определения уравнения ![]() .
.
Пример 22. Решите уравнение ![]() .
.
Решение. ![]() .
.
Решим совокупность уравнений:
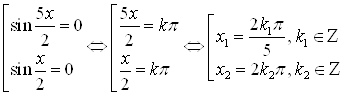 .
.
Если приравнять ![]() и
и ![]() , то увидим, что эти решения образуют одно множество:
, то увидим, что эти решения образуют одно множество: ![]() .
.
Ответ. 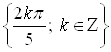 .
.
При решении уравнений методом разложения на множители возможно появление посторонних корней. Чтобы исключить ошибки в ответе, рекомендуется находить ОДЗ.
В ответе необходимо исключить решения, не удовлетворяющие ОДЗ.
Пример 23. Решите уравнение ![]() .
.
Решение. Найдем ОДЗ: ![]() . Решим совокупность уравнений:
. Решим совокупность уравнений:  .
.
Заметим, что решения ![]() не входят в ОДЗ (ОДЗ:
не входят в ОДЗ (ОДЗ: ![]() ). Поэтому ответом будут только решения
). Поэтому ответом будут только решения ![]() .
.
Ответ. 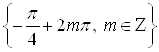 .
.
4. Метод понижения степени
При решении уравнений используют формулы понижения степени:  ;
; 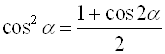 .
.
Пример 24. Решите уравнение ![]() .
.
Решение. Используем формулы понижения степени, получим: ![]()
![]() . Применим к первым двум слагаемым формулу преобразования суммы одноименных тригонометрических функций в произведение:
. Применим к первым двум слагаемым формулу преобразования суммы одноименных тригонометрических функций в произведение: ![]() .
.
Получим, ![]() .
.
Решим совокупность уравнений:
 .
.
Ответ. 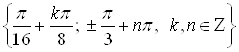 .
.
Пример 25. Решите уравнение ![]() .
.
Решение. Степень можно понизить выделением квадрата суммы:
![]() .
.
Используя формулы ![]() и
и ![]() , получим:
, получим:
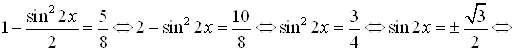
![]() .
.
Ответ. 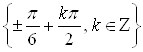 .
.
5. Метод преобразования произведения функций в сумму
При решении уравнений целесообразно использовать следующие формулы:
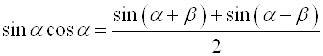 ;
;
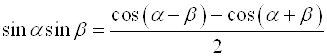 ;
;
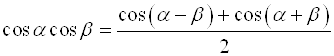 .
.
Пример 26. Решите уравнение ![]() .
.
Решение. Используем формулу преобразования произведения тригонометрических функций в сумму, получим:
![]() .
.
Теперь используем формулу ![]() и выполним обратное преобразование. Получим:
и выполним обратное преобразование. Получим: ![]() . Решим совокупность уравнений:
. Решим совокупность уравнений:
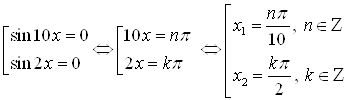 .
.
Решения ![]() являются подмножеством решений
являются подмножеством решений ![]() (при
(при ![]() решения
решения ![]() и
и ![]() совпадают). Поэтому в ответе запишем только
совпадают). Поэтому в ответе запишем только ![]() .
.
Ответ. 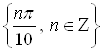 .
.
6. Метод введения вспомогательного аргумента
Этот метод удобно использовать при решении уравнений вида ![]() , где
, где ![]() ,
, ![]() .
.
Разделим обе части уравнения на первый коэффициент: 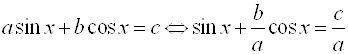 . Теперь заменим
. Теперь заменим ![]() через
через ![]() (
(![]() – это вспомогательный аргумент или вспомогательный угол), т. е.:
– это вспомогательный аргумент или вспомогательный угол), т. е.: 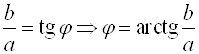 .
.
Подставим в уравнение вместо ![]() значение
значение 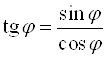 и освободим левую часть от знаменателя:
и освободим левую часть от знаменателя:
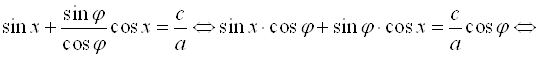
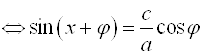 .
.
Уравнение имеет решение только при  .
.
Определим ![]() через коэффициенты
через коэффициенты ![]() ,
, ![]() ,
, ![]() :
:
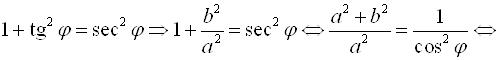
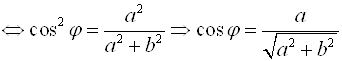 .
.
Аналогично найдем: 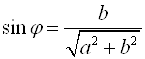 .
.
Подставим значение ![]() в уравнение
в уравнение 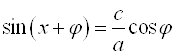 . Получим:
. Получим:
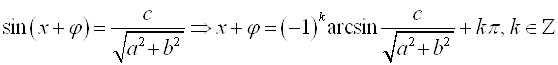 .
.
При решении тригонометрических уравнений методом введения вспомогательного аргумента используют следующие формулы:
1) ![]() ;
;
2) 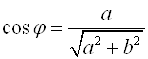 ;
; 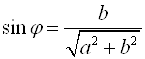 ;
;
3) 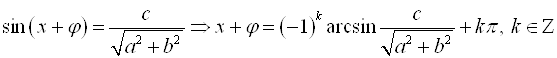 .
.
Пример 27. Решите уравнение ![]() .
.
Решение. В нашем случае ![]() ,
, ![]() ,
, ![]() . Найдем
. Найдем 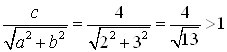 . Тогда исходное уравнение можно привести к уравнению
. Тогда исходное уравнение можно привести к уравнению  .
.
Ответ. ![]() .
.
Пример 28. Решите уравнение 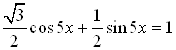 .
.
Решение. Вспомогательный угол можно ввести следующим образом: 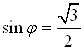 ,
, ![]() , тогда
, тогда ![]() .
.
Подставим значения 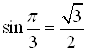 и
и ![]() в уравнение. Получим:
в уравнение. Получим:
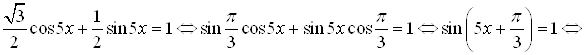
![]() .
.
Ответ. 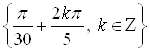 .
.
Пример 29. Решите уравнение ![]() .
.
Решение. По формулам 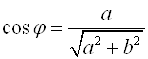 и
и 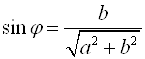 найдем значения
найдем значения 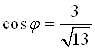 и
и 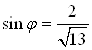 .
.
Преобразуем исходное уравнение: ![]()
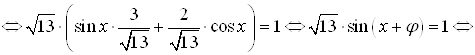
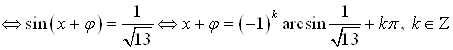 .
.
Мы знаем, что 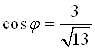 ,
, 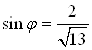 ,
, ![]() , тогда
, тогда ![]() или
или 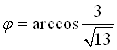 , или
, или 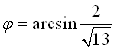 . Поэтому решение уравнения можно записать так:
. Поэтому решение уравнения можно записать так:
А) 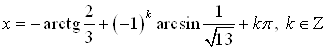 ; или
; или
Б) 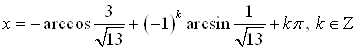 ; или
; или
В) 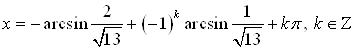 .
.
Ответ. 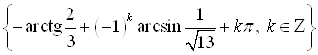 .
.
7. Метод универсальной подстановки 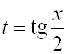
При использовании метода универсальной подстановки значения ![]() ,
, ![]() ,
, ![]() и
и ![]() удобно выражать через
удобно выражать через ![]() по следующим формулам:
по следующим формулам:
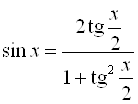 ;
; 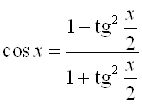 ;
; 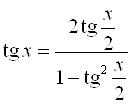 ;
; 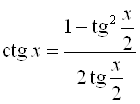 .
.
Использование универсальной подстановки возможно при 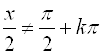 , т. е.
, т. е. ![]() . Поэтому при решении нужно проверять, не являются ли числа вида
. Поэтому при решении нужно проверять, не являются ли числа вида ![]() ,
, ![]() решениями исходного уравнения.
решениями исходного уравнения.
Пример 30. Решите уравнение ![]() .
.
Решение. Заменим ![]() и
и ![]() на
на ![]() , получим:
, получим:
 .
.
Тогда из уравнения ![]() получаем:
получаем: ![]() .
.
Из уравнения ![]() получаем:
получаем: ![]() .
.
Проверим, удовлетворяют ли исходному уравнению числа ![]() . Для этого подставим
. Для этого подставим ![]() в исходное уравнение:
в исходное уравнение: ![]() ; значит, числа
; значит, числа ![]() не являются решениями исходного уравнения.
не являются решениями исходного уравнения.
Ответ. 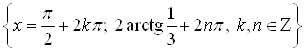 .
.
Пример 31. Решите уравнение ![]() .
.
Решение. Найдем ОДЗ уравнения: 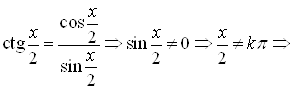 .
.
![]() Используем подстановку
Используем подстановку ![]() :
:
![]()
![]() .
.
Дискриминант трехчлена ![]() меньше нуля
меньше нуля ![]() , следовательно:
, следовательно: ![]() .
.
Тогда ![]()
Проверим, удовлетворяет ли значение ![]() исходному уравнению:
исходному уравнению: ![]() .
.
Ответ. 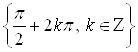 .
.
8. Метод подстановки ![]()
Подстановку удобно выполнять, когда в уравнении есть сумма (разность) и произведение функций синуса и косинуса.
Для того чтобы выразить через ![]() произведение синуса на косинус, возведем в квадрат сумму
произведение синуса на косинус, возведем в квадрат сумму ![]() , а затем определим произведение
, а затем определим произведение ![]() через
через ![]() :
:
![]()
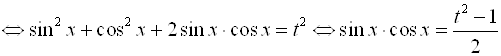 .
.
Аналогично для ![]()
![]()
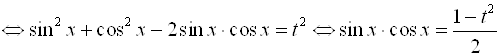 .
.
Следовательно, имеем две подстановки:
1) 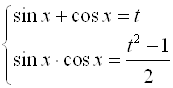 ; 2)
; 2) 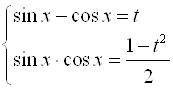 .
.
Пример 32. Решите уравнение ![]() .
.
Решение. Используем вторую подстановку:
![]() .
.
Тогда ![]() ,
, ![]() . Но
. Но ![]() , поэтому
, поэтому ![]() :
: ![]() .
.
Для решения этого уравнения заменим ![]() через
через ![]() и по формуле
и по формуле ![]() преобразуем разность синусов в произведение:
преобразуем разность синусов в произведение:

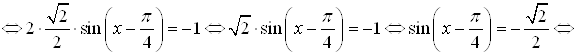
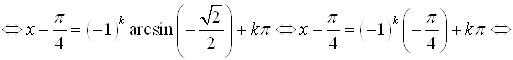
![]() .
.
Ответ. 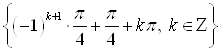 .
.
| < Предыдущая | Следующая > |
|---|