102. Простейшие тригонометрические уравнения
Тригонометрические уравнения – это уравнения, в которых неизвестная величина находится под знаком тригонометрических функций.
Простейшие тригонометрические уравнения – это уравнения вида ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решить простейшее тригонометрическое уравнение – это значит найти множество всех углов, для которых функция равна ![]() .
.
Если тригонометрическое уравнение не является простейшим, то его нужно привести к одному или нескольким простейшим уравнениям. Для этого используют тождественные преобразования.
Рассмотрим решение простейших тригонометрических уравнений.
1. Уравнение ![]() .
.
Мы знаем, что ![]() , поэтому уравнение имеет решение только, при
, поэтому уравнение имеет решение только, при ![]() .
.
Известно, что ![]() – это ордината единичного вектора. Поэтому, отложим величину
– это ордината единичного вектора. Поэтому, отложим величину ![]() на оси
на оси ![]() и изобразим тригонометрическую окружность. Тогда получим два угла (
и изобразим тригонометрическую окружность. Тогда получим два угла (![]() и
и ![]() ), синус которых равен
), синус которых равен ![]() (рис. 8.9).
(рис. 8.9).
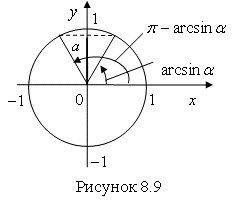
С учетом периодичности синуса получим два множества решений: ![]() и
и ![]() , где
, где ![]() .
.
Приведем подобные члены в выражении для ![]() , получим:
, получим: ![]() ,
, ![]() .
.
Объединим полученные множества решений (![]() – четные числа;
– четные числа; ![]() – нечетные числа), получим:
– нечетные числа), получим:
![]() ,
, ![]() ;
; 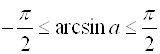 .
.
При четном ![]()
![]() , получим множество решений
, получим множество решений ![]() ; при нечетном
; при нечетном ![]()
![]() получим множество решений
получим множество решений ![]() . Однако, если
. Однако, если ![]() ,
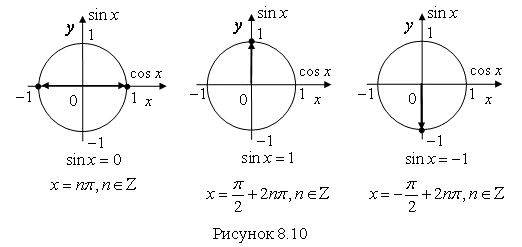
, ![]() , то этой формулой пользоваться нецелесообразно. Рассмотрим соответствующие решения, используя тригонометрическую окружность (рис. 8.10).
, то этой формулой пользоваться нецелесообразно. Рассмотрим соответствующие решения, используя тригонометрическую окружность (рис. 8.10).
Пример 13. Решите уравнение 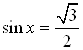 .
.
Решение. 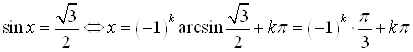 .
.
Ответ. ![]() ,
, ![]() .
.
Пример 14. Решите уравнение 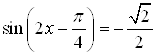 .
.
Решение. 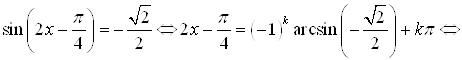
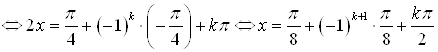 .
.
Запишем результат в виде двух множеств решений:
При ![]() , тогда
, тогда ![]() ,
, ![]() ;
;
При ![]() , тогда
, тогда 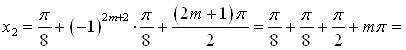
![]() ,
, ![]() .
.
Ответ. ![]() ,
, ![]() .
.
2. Уравнение ![]() .
.
Уравнение имеет решение при ![]() . Рассмотрим тригонометрическую окружность. Отложим на оси
. Рассмотрим тригонометрическую окружность. Отложим на оси ![]() величину
величину ![]() и получим два угла (
и получим два угла (![]() и
и ![]() ), косинус которых равен
), косинус которых равен ![]() (рис. 8.11).
(рис. 8.11).
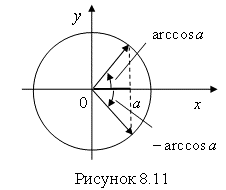
С учетом периодичности косинуса получим два множества решений: ![]() и
и ![]() ,
, ![]() .
.
Эти два множества можно объединить в одно:
![]() , где
, где ![]() .
.
Для частных случаев ![]() ;
; ![]() :
:
А) 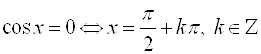 ;
;
Б) ![]() ;
;
В) ![]() (рис. 8.12).
(рис. 8.12).
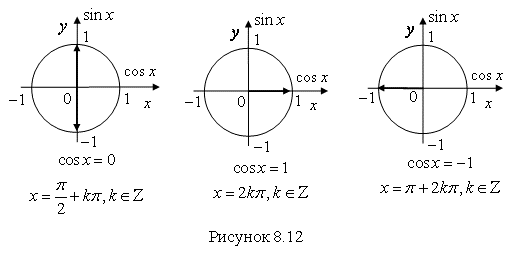
Пример 15. Решите уравнение ![]() .
.
Решение. При решении уравнений вида ![]() где
где ![]() важно помнить, что:
важно помнить, что: ![]()
![]() . Поэтому запишем:
. Поэтому запишем:

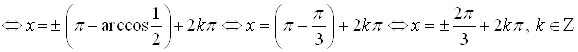 .
.
Ответ. 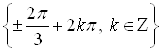 .
.
3. Уравнения ![]() и
и ![]() .
.
Известно, что функции тангенс и котангенс – функции неограниченные. Рассмотрим тригонометрическую окружность. Проведем оси тангенсов и котангенсов. Отложим на них величину ![]() . Найдем значения углов при различных значениях
. Найдем значения углов при различных значениях ![]() (рис. 8.13).
(рис. 8.13).
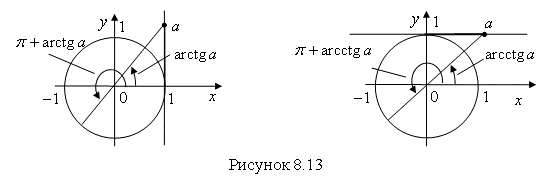
Для произвольного ![]() получим:
получим:
![]() , где
, где 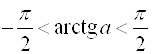 ;
;
![]() , где
, где  .
.
Для частных случаев ![]() ;
; ![]() получим:
получим:
А) ![]() ;
; 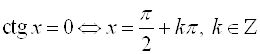 ;
;
Б) 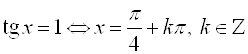 ;
; 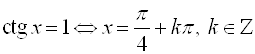 ;
;
В) 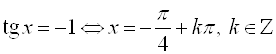 ;
; 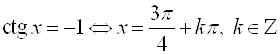 .
.
Пример 16. Решите уравнение 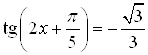 .
.
Решение. При решении уравнений, в которые входят функции ![]() и
и ![]() , находим ОДЗ:
, находим ОДЗ: 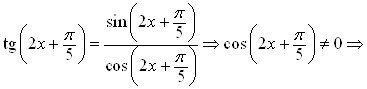
![]() .
.
Решим исходное уравнение 
![]() .
.
Ответ. 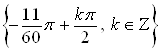 .
.
Пример 17. Решите уравнение 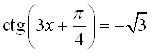 .
.
Решение. Найдем ОДЗ: 
![]() .
.
Решим исходное уравнение:
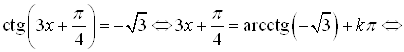
![]()
![]() .
.
Ответ. 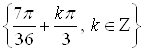
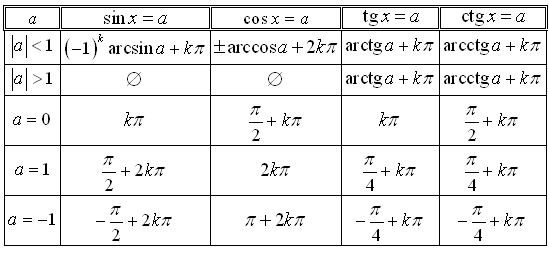
Приведем обобщенную таблицу решений простейших тригонометрических уравнений (табл. 8.4). Во всех формулах таблицы ![]() .
.
Таблица 8.4 – Решение простейших тригонометрических уравнений
| < Предыдущая | Следующая > |
|---|