098. Определение тригонометрических функций
Рассмотрим окружность единичного радиуса с центром в начале плоской системы координат ![]() (рис. 8.4). Такая окружность называется Единичной окружностью Или Тригонометрической окружностью.
(рис. 8.4). Такая окружность называется Единичной окружностью Или Тригонометрической окружностью.
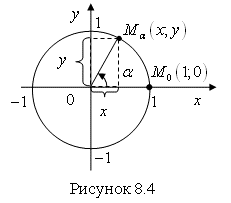
Отметим на оси ![]() справа от начала координат точку
справа от начала координат точку ![]() , лежащую на тригонометрической окружности:
, лежащую на тригонометрической окружности: ![]() .
.
Радиус ![]() называется начальным радиусом. Точка
называется начальным радиусом. Точка ![]() переходит в точку
переходит в точку ![]() при повороте начального радиуса
при повороте начального радиуса ![]() около центра
около центра ![]() на угол
на угол ![]() (
(![]() – это единичный радиус-вектор).
– это единичный радиус-вектор).
Синус угла – это отношение ординаты точки ![]() к радиусу окружности:
к радиусу окружности: 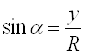 .
.
Косинус угла – это отношение абсциссы точки ![]() к радиусу окружности:
к радиусу окружности: 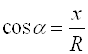 .
.
Радиус единичной окружности равен единице ![]() , поэтому:
, поэтому: ![]() ;
; ![]() . Синус угла
. Синус угла ![]() – это ордината единичного вектора; косинус угла
– это ордината единичного вектора; косинус угла ![]() – это абсцисса единичного вектора.
– это абсцисса единичного вектора.
Ось ![]() называют Осью синусов, а ось
называют Осью синусов, а ось ![]() называют Осью косинусов.
называют Осью косинусов.
Тангенс угла ![]() – это отношение ординаты точки
– это отношение ординаты точки ![]() к ее абсциссе:
к ее абсциссе: 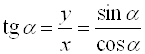 .
.
Прямая ![]() называется Осью тангенсов (рис. 8.5).
называется Осью тангенсов (рис. 8.5).
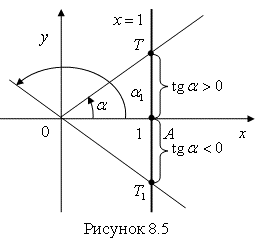
Тангенс угла ![]() равен ординате соответствующей точки
равен ординате соответствующей точки ![]() на оси тангенсов.
на оси тангенсов.
Котангенсом угла ![]() называется отношение абсциссы точки
называется отношение абсциссы точки ![]() к ее ординате:
к ее ординате: 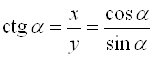 .
.
Прямая ![]() называется Осью котангенсов (рис. 8.6)
называется Осью котангенсов (рис. 8.6)
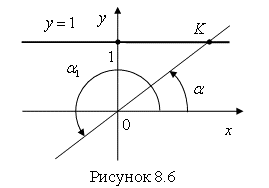
Котангенс угла ![]() равен абсциссе соответствующей точки
равен абсциссе соответствующей точки ![]() на оси котангенсов.
на оси котангенсов.
Кроме функций синуса, косинуса, тангенса и котангенса используются еще две тригонометрические функции угла ![]() – это секанс и косеканс.
– это секанс и косеканс.
Секанс угла ![]() – это величина, обратная
– это величина, обратная ![]() :
:
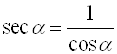 ;
; ![]() .
.
Косеканс угла ![]() – это величина, обратная
– это величина, обратная ![]() :
:
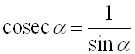 ;
; ![]() .
.
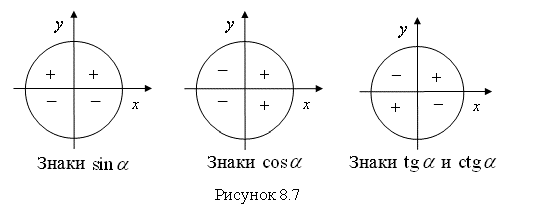
Рассмотрим знаки тригонометрических функций ![]() ,
, ![]() ,
, ![]() ,
, ![]() в различных четвертях (квадрантах) (рис. 8.7)
в различных четвертях (квадрантах) (рис. 8.7)
Пример 3. Определите знак выражений: а) ![]() ; б)
; б) ![]() .
.
Решение. Отметим углы в 2 и 6 радиан на тригонометрической окружности (рис. 8.8)
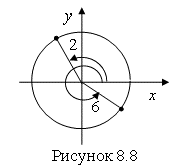
Мы знаем, что ![]() и
и ![]() Радиан. Поэтому
Радиан. Поэтому ![]() ;
; ![]() . Поэтому угол
. Поэтому угол ![]() оканчивается во II четверти, а угол
оканчивается во II четверти, а угол ![]() оканчивается в III четверти. Тогда
оканчивается в III четверти. Тогда ![]() ;
; ![]() .
.
Ответ. а) ![]() ; б)
; б) ![]() .
.
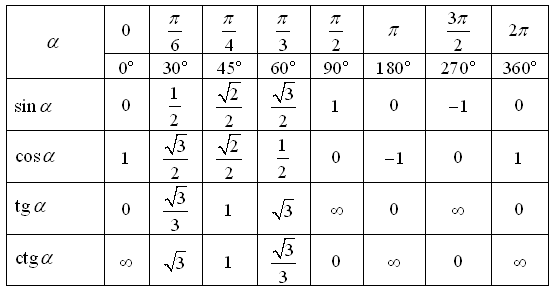
Рассмотрим значения тригонометрических функций некоторых углов (табл. 8.2).
Таблица 8.2 – Значения тригонометрических функций некоторых углов
Символ ![]() (бесконечность) означает, что
(бесконечность) означает, что ![]() или
или ![]() при соответствующих значениях аргумента не определены и принимают сколь угодно большие значения по модулю.
при соответствующих значениях аргумента не определены и принимают сколь угодно большие значения по модулю.
Пример 4. Найдите значение выражений:
А) ![]() ;
;
Б) ![]() .
.
Решение. а) ![]()
![]()
Б) ![]() .
.
Ответ. а) ![]() ; б)
; б) ![]() .
.
Пример 5. Упростите выражение: ![]() .
.
Решение. ![]() .
.
Ответ. ![]() .
.
| < Предыдущая | Следующая > |
|---|