094. Логарифмические неравенства

Неравенство, которое содержит переменную под знаком логарифма или в основании логарифма, называется Логарифмическим.

Решение логарифмических неравенств обычно сводится к решению неравенств вида: . Это простейшее логарифмическое неравенство.

При решении логарифмических неравенств нужно помнить следующее:

1) выражение с переменной под знаком логарифма может быть только положительным;

2) логарифмическая функция монотонно возрастает при и монотонно убывает при .

Решение логарифмических неравенств сводится к решению системы неравенств.

Если основание логарифма содержит переменную, то решение неравенства сводится к решению двух систем неравенств:

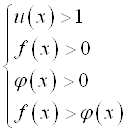А)  б)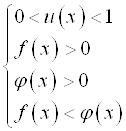 

Решение исходного неравенства – это объединение множеств решений этих двух систем.

Пример 40. Решите неравенство .

Решение. (ОДЗ: ).

В этом примере для решения неравенства не нужно записывать две системы неравенств, которые приведены выше. Из условия мы знаем, что основание данного логарифма "2", а это больше единицы, поэтому здесь достаточно записать обе части неравенства как логарифмы с одинаковым основанием "2" и получить линейное неравенство:

.

Проверим, принадлежит ли найденное решение ОДЗ исходного неравенства и убедимся, что это решение входит в ОДЗ неравенства.

Ответ. .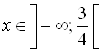

Пример 41. Решите неравенство .

Решение. Основание логарифмов больше "1", поэтому можно записать только одну систему неравенств:

.

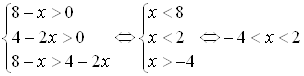Ответ. .

Пример 42. Решите неравенство .

Решение. Запишем логарифм по основанию "4" как логарифм по основанию "2", получим: .

Пусть , тогда запишем исходное неравенство так: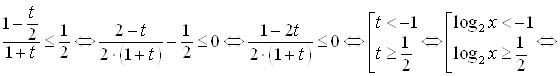

.

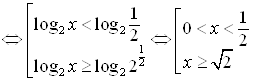Ответ. .

Пример 43. Решите неравенство .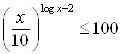

Решение. Прологарифмируем неравенство по основанию "10". Знак неравенства не изменится, т. к. , поэтому:

.

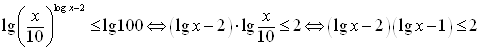Пусть , тогда или .

Ответ. .

Пример 44. Решите неравенство .

Решение. Запишем неравенство так: .

Решение этого неравенства будет объединение решений систем а) и б).

А) ;

Б) .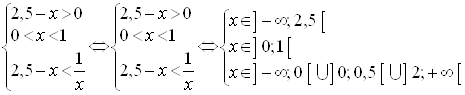

Ответ. .

Пример 45. Решите неравенство .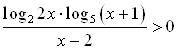

Решение. ОДЗ: .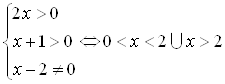

Найдем значения , при которых каждый множитель обращается в ноль:

;

;

.

Отметим на числовой прямой точки: ; ; (рис. 7.1).

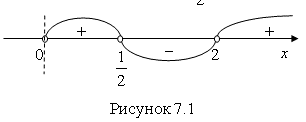
Числовая прямая с учетом ОДЗ разбивается на три промежутка:

; ; .

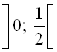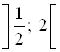Обозначим 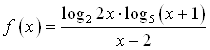и определим знак на каждом из промежутков. Для этого возьмем любое значение из каждого интервала, подставим в и узнаем знак на этом интервале.

1) ; 2) ; 3) .

Так, при 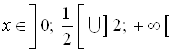, значит это и есть решение исходного неравенства.

Ответ. .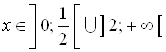

< Предыдущая		Следующая >