093. Показательные неравенства

Неравенство, которое содержит переменную в показателе степени, называется Показательным неравенством.

Общий вид показательного неравенства: .

Решение любого показательного неравенства можно привести к решению неравенства с одинаковым основанием: .

Решение такого неравенства основано на свойстве монотонности показательной функции: при показательная функция монотонно возрастает; при показательная функция монотонно убывает. Поэтому могут быть два случая:

А) , ;

Б) , .

Если выражение с переменной находится и в основании, и в показателе степени, то это неравенство называется Показательно-степенным. Решение такого неравенства сводится к решению системы неравенств.

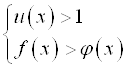При решении неравенства рассматривают два случая: а) ; б) .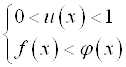

Решением показательного неравенства будет объединение множеств решений этих систем.

Пример 34. Решите неравенство .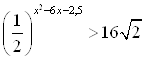

Решение. Правую часть неравенства запишем так: 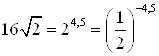. Тогда исходное неравенство будет иметь вид: .

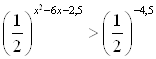Основание , поэтому это неравенство равносильно квадратному неравенству или . Решением этого неравенства будут: ; , а решением исходного неравенства будет: .

Ответ. .

Пример 35. Решите неравенство .

Решение. Преобразуем обе части неравенства: . Основание , поэтому можно записать: .

Ответ. .

Пример 36. Решите неравенство .

Решение. Исходное неравенство запишем так: .

В левой части неравенства находятся функции, однородные относительно и . Разделим обе части исходного неравенства на . Получим: .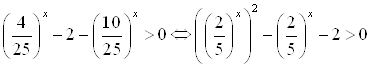

Пусть 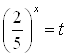, , тогда 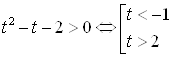. Т. к. , тогда не может быть решением неравенства. Если 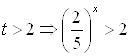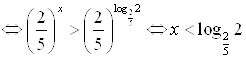будет решением исходного неравенства.

Ответ. .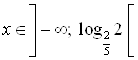

Пример 37. Решите неравенство .

Решение. Запишем исходное неравенство так: . Решением этого неравенства будет объединение решений нижеприведенных систем 1) и 2).

1) 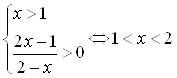; 2) .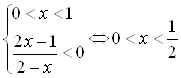

Ответ. .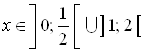

Пример 38. Решите неравенство .

Решение. (ОДЗ: ). Это показательно-степенное неравенство равносильно двум системам неравенств:

1) 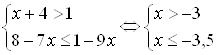; т. е. .

2) .

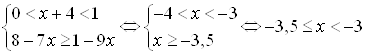Значение принадлежит ОДЗ исходного неравенства, т. к. . Поэтому – это решение исходного неравенства.

Ответ. .

Пример 39. Решите неравенство .

Решение. Найдем ОДЗ: .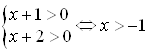

Разделим обе части исходного неравенства на .

Получаем неравенство, равносильное исходному: .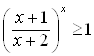

Рассмотрим три возможных случая в зависимости от величины основания:

1) .

2)  .

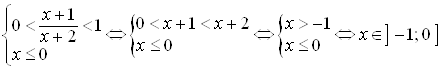3).

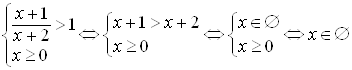Ответ. .

< Предыдущая		Следующая >