091. Логарифмические уравнения. Методы их решения
Уравнение называется Логарифмическим, если переменная в нем содержится под знаком логарифма или в основании логарифма.
Например, уравнения 
; 
; 
– это логарифмические уравнения.
Решение логарифмических уравнений основано на свойствах логарифмической функции.
Простейшие логарифмические уравнения – это уравнения вида: а) 
; б) 
; в) 
; г) ; д) 
.
Рассмотрим решение некоторых простейших логарифмических уравнений разными методами.
I. Решение простейших логарифмических уравнений с использованием свойств логарифма
А) 
.
Пример 20. Решите уравнение 
.
Решение. (ОДЗ: 
); 
.
Ответ. 
.
Б) 
.
Пример 21. Решите уравнение 
.
Решение. (ОДЗ: 
); 
.
Ответ. 
.
В) 
.
Пример 22. Решите уравнение 
.
Решение. 
.
.
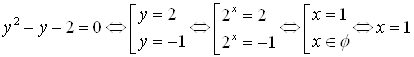Проверка. Если 
значит 
– это корень исходного уравнения.
Ответ. 
.
Г)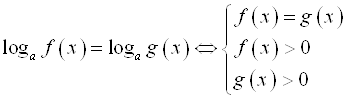 
, где 
.
Пример 23. Решите уравнение 
.
Решение. 
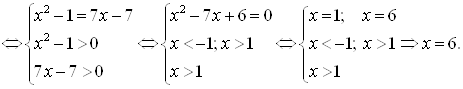
– это единственный корень исходного уравнения.
Ответ. 
.
Д)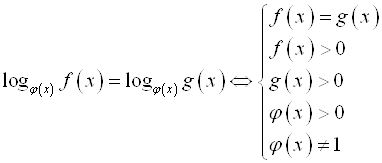 
.
Пример 24. Решите уравнение 
.
Решение. 
.
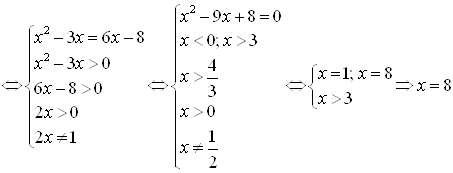Ответ. 
.
II. Решение логарифмических уравнений потенцированием.
Пример 25. Решите уравнение 
.
Решение. Сделаем преобразования:
.
Решаем систему: 
.
Ответ. 
.
III. Решение уравнений с применением основного логарифмического тождества 
.
Пример 26. Решите уравнение 
.
Решение. Преобразуем левую часть уравнения: 
, тогда 
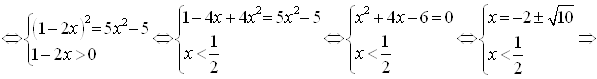
– это единственный корень исходного уравнения.
Ответ. 
.
IV. Решение логарифмических уравнений методом замены переменной.
Пример 27. Решите уравнение 
.
Решение. ОДЗ: .
Поскольку 
, значит
.
Пусть 
, тогда: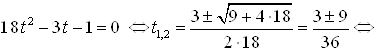 
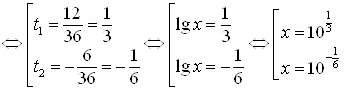
Ответ.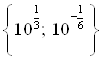 
.
V. Решение уравнений методом логарифмирования.
Пример 28. Решите уравнение 
.
Решение. (ОДЗ: ). Прологарифмируем обе части уравнения и сделаем преобразования: 
.
Пусть 
, получим: 
.
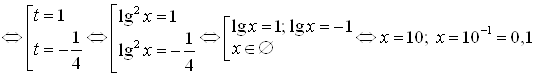Ответ. 
.
VI. Решение уравнений методом деления обеих частей на показательно-логарифмическую функцию.
Пример 29. Решите уравнение 
.
Решение. (ОДЗ: ). 
.
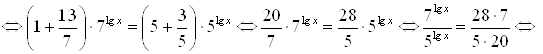
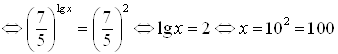Ответ. 
.
VII. Решение уравнений с использованием формулы перехода к другому основанию.
Пример 30. Решите уравнение 
.
Решение. (ОДЗ: ). Перейдем к основанию 2:
.
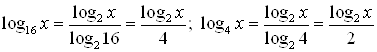Пусть 
, тогда 
.
Ответ. 
.
| < Предыдущая | Следующая > |
|---|
