090. Показательные уравнения. Методы их решения
Показательные уравнения – это такие уравнения, в которых переменная содержится в показателе степени.
Например, ![]() ;
; ![]() ;
; ![]() – это показательные уравнения.
– это показательные уравнения.
Решение показательных уравнений основано на свойствах показательной функции. Рассмотрим решение некоторых видов показательных уравнений разными методами.
I. Метод приведения к одинаковому основанию
А) ![]() ,
, ![]() ,
, ![]() .
.
Если равны степени с одинаковыми положительными основаниями (не равными единице), то равны и показатели степеней, т. е. ![]() .
.
Б) ![]() ,
, ![]() ,
, ![]() .
.
Степень с положительным основанием равна единице, если показатель этой степени равен нулю, т. е. ![]() , тогда
, тогда ![]() , значит
, значит ![]() .
.
Пример 10. Решите уравнение ![]() .
.
Решение. Приведем обе части уравнения к одинаковому основанию "2" и решим полученное линейное уравнение:
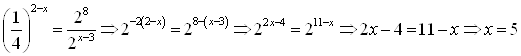 .
.
Ответ. ![]() .
.
Пример 11. Решить уравнение ![]() .
.
Решение. ![]() .
.
Ответ. ![]() .
.
II. Метод деления обеих частей уравнения на ![]() Или
Или ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пример 12. Решите уравнение ![]() .
.
Решение. 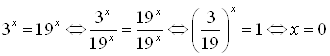 .
.
Ответ. ![]() .
.
III. Метод логарифмирования обеих частей уравнения по одному и тому же основанию
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для того чтобы найти решения этого уравнения, нужно сделать преобразования, а потом логарифмировать обе части уравнения по одному и тому же основанию.
Пример 13. Решите уравнение ![]() .
.
Решение. Преобразуем уравнение: 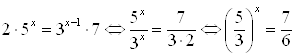 . Прологарифмируем обе части уравнения по основанию
. Прологарифмируем обе части уравнения по основанию ![]() :
:
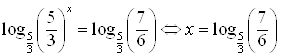
Ответ. 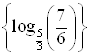 .
.
Пример 14. Решите уравнение ![]() .
.
Решение. Прологарифмируем исходное уравнение по основанию "7" (можно логарифмировать и по основанию "8" или по любому положительному основанию, не равному "1").
![]()
![]() . Решим это квадратное уравнение, найдем его корни:
. Решим это квадратное уравнение, найдем его корни: ![]() . Это и будут решения исходного уравнения.
. Это и будут решения исходного уравнения.
Ответ. ![]() .
.
IV. Метод вынесения общего множителя за скобки
Пример 15. Решите уравнение ![]() .
.
Решение. Преобразуем уравнение: ![]() .
.
Вынесем общий множитель ![]() за скобки:
за скобки: ![]()
![]() .
.
Ответ. ![]() .
.
V. Метод приведения к квадратному уравнению
А) Уравнения вида ![]() (
(![]() ,
, ![]() ) с помощью подстановки
) с помощью подстановки ![]() можно привести к квадратному уравнению
можно привести к квадратному уравнению ![]() .
.
Пример 16. Решите уравнение ![]() .
.
Решение. Пусть ![]() , тогда
, тогда ![]() . Подставим эти значения в исходное уравнение, получим:
. Подставим эти значения в исходное уравнение, получим: ![]()
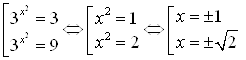 .
.
Ответ. ![]() .
.
Б) Уравнения вида 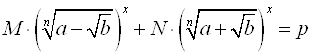 , где
, где ![]() приводят к квадратным уравнениям путем замены:
приводят к квадратным уравнениям путем замены: 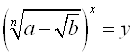 или
или 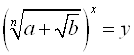 .
.
Пример 17. Решите уравнение ![]() .
.
Решение. Делаем замену: 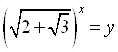 . Получим:
. Получим:
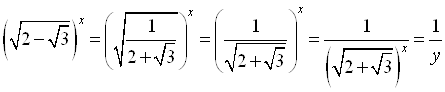 .
.
Тогда исходное уравнение эквивалентно уравнению:
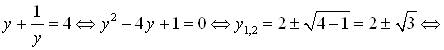
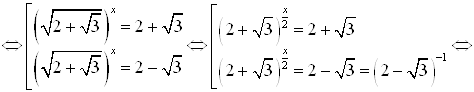
 .
.
Ответ. ![]() .
.
VI. Метод введения новой переменной
Уравнения вида ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() , а сумма показателей степеней чисел
, а сумма показателей степеней чисел ![]() и
и ![]() в каждом члене равна
в каждом члене равна ![]() , решаем делением каждого члена уравнения на
, решаем делением каждого члена уравнения на ![]() (
(![]() ):
):
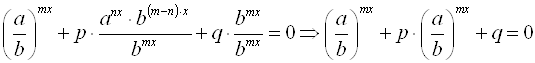 .
.
Полученное уравнение решаем методом замены перемены 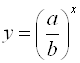 , что приводит к уравнению
, что приводит к уравнению ![]() . Его корнями будут
. Его корнями будут ![]() ,
, ![]() , ...,
, ..., ![]() . Решая уравнения:
. Решая уравнения: 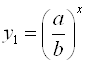 , ...,
, ..., 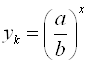 , получим
, получим ![]() значений
значений ![]() .
.
Пример 18. Решите уравнение ![]() .
.
Решение. Запишем данное уравнение так: ![]() .
.
Разделим каждый член уравнения на ![]() , получим:
, получим: 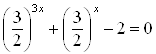 .
.
Пусть 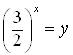 ,
, ![]() , тогда
, тогда ![]()
![]() .
.
Уравнение ![]() не имеет действительных корней, т. к. его дискриминант менше нуля
не имеет действительных корней, т. к. его дискриминант менше нуля ![]() . Поэтому,
. Поэтому, 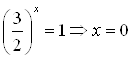 .
.
Ответ. ![]() .
.
Уравнения вида ![]() называются Показательно-степенными.
называются Показательно-степенными.
При решении таких уравнений проверяют случаи, когда основание степени может быть равно: ![]() ;
; ![]() ;
; ![]() , потому что корни этих трех уравнений могут быть корнями данного уравнения.
, потому что корни этих трех уравнений могут быть корнями данного уравнения.
Если ![]() ;
; ![]() ;
; ![]() , то используем условие равенства степеней с равными основаниями:
, то используем условие равенства степеней с равными основаниями: ![]() . В этом случае обязательно нужно сделать проверку, т. к. левая или правая части уравнения могут не иметь смысла.
. В этом случае обязательно нужно сделать проверку, т. к. левая или правая части уравнения могут не иметь смысла.
Пример 19. Решите уравнение ![]() .
.
Решение. Рассмотрим случаи равенства основания единице, минус единице и нулю: ![]() ;
; ![]() ;
; ![]() .
.
А) ![]()
![]() . Проверим это значение:
. Проверим это значение: ![]() .
.
Значит, ![]() – это корень уравнения.
– это корень уравнения.
Б) ![]()
![]() . Проверим это значение:
. Проверим это значение: ![]() .
.
Значит, ![]() – это корень уравнения.
– это корень уравнения.
В) ![]()
![]() . Проверим это значение:
. Проверим это значение: ![]() .
.
Значит, ![]() – это не корень уравнения.
– это не корень уравнения.
Г) Пусть ![]() ;
; ![]() ;
; ![]() . Тогда
. Тогда ![]()
![]() . Проверим эти значение:
. Проверим эти значение:
![]()
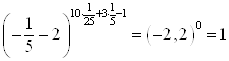 ;
;
![]()
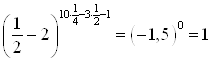 .
.
Значит, ![]() и
и ![]() – это корни уравнения.
– это корни уравнения.
Ответ. 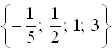 .
.
| < Предыдущая | Следующая > |
|---|