088. Свойства логарифмов

1) (основное логарифмическое тождество);

2) (логарифм по основанию от числа равен единице);

3) (логарифм по основанию от единицы равен нулю);

4) , если , (логарифм произведения двух положительных множителей равен сумме их логарифмов);

5) 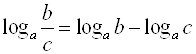, если , (логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя);

6) , если (логарифм степени положительного числа равен произведению показателя степени на логарифм основания степени);

7) 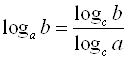, если (формула перехода к новому основанию);

7а) если , тогда ;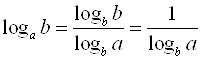

8) (если основание логарифма и число, стоящее под знаком логарифма, возвести в одну и ту же степень, не Равную нулю, то значение логарифма не изменится);

9) 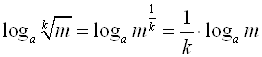(логарифм корня из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня);

10) 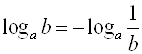 (логарифмы взаимно обратных чисел по одинаковому основанию отличаются только знаком);

11) .

Пример 3. Упростите: а) ; б) ; в) ;

Г) .

Решение. а) Сделаем преобразования показателя степени:

.

Б) Выполним преобразования показателя степени, для этого используем свойства логарифма:

,

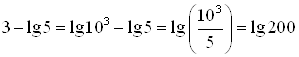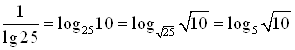, тогда:

.

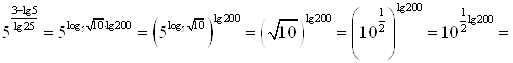
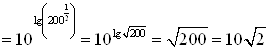В) Используя свойство логарифма 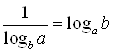, получим:

.

Г) Запишем все множители через основание 10, получим:

.

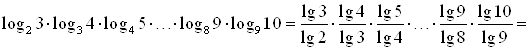
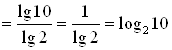Ответ. а) ; б) ; в) ;

Г) .

Пример 4. А) Найдите , если ; ;

Б) найдите , если ; .

Решение. а) Используя свойства логарифма, выполним преобразования данного выражения: ; если ; , тогда .

Б) Используя свойства логарифма, выполним преобразования данного выражения: ; если ; , тогда .

Ответ. а) ; б) .

Пример 5. Упростите .

Решение. Представим выражение под знаком логарифма в виде степени: , тогда:

.

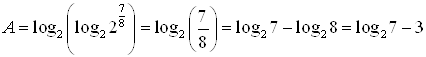Ответ..

Пример 6. Вычислите .

Решение. Используя свойства логарифма, преобразуем выражения: 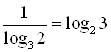; ; 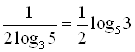тогда

.

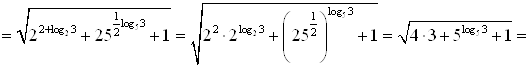
Ответ..

< Предыдущая		Следующая >