084. Графическое решение неравенств и систем неравенств

Неравенства с одной или двумя переменными и системы неравенств можно решить графически.

Рассмотрим графическое решение неравенства с одной переменной Для этого построим в одной системе координат графики функций и .

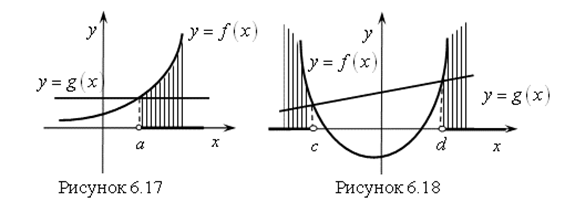
Решением неравенства будет множество значений переменной , при которых график функции находится выше графика функции , так как . Это показано на рисунке 6.17 (здесь решение: ) и на рисунке 6.18 (здесь решение: ).

Рассмотрим неравенство Известно, что решением неравенства с двумя переменными есть множество точек плоскости, координаты которых удовлетворяют этому неравенству. Рассмотрим на примерах решение некоторых неравенств с двумя переменными.

Пример 24. Решите графически неравенство .

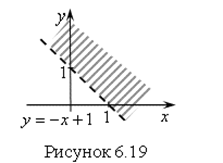
Решение. Запишем неравенство в виде . Построим прямую .

Ответ. Координаты точек плоскости, которые лежат выше этой прямой, будут решением неравенства (на рис. 6.19 – это заштрихованная область).

Пример 25. Решите неравенство

.

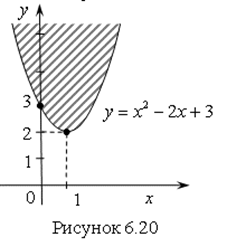
Решение. Запишем неравенство в виде . Построим параболу – это график функции .

Ответ. Решение неравенства – это множество точек плоскости, лежащих на параболе и выше нее (рис. 6.20).

Пример 26. Решите неравенство

.

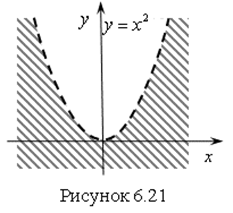
Решение. Запишем неравенство в виде . Построим параболу .

Ответ. Решение неравенства – это множество точек плоскости, которые лежат в заштрихованной области (ниже построенной параболы) (рис. 6.21).

При решении систем неравенств с двумя переменными находят пересечение областей решений этих неравенств.

Пример 27. Решите графически систему неравенств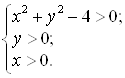

Решение. Решение первого неравенства – это множество точек плоскости, которые лежат вне окружности . Решение второго неравенства – это множество точек выше оси (верхняя полуплоскость). Решение третьего неравенства – это множество точек справа от оси (правая полуплоскость).

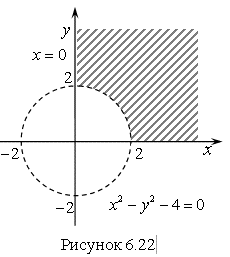
Решением исходной системы неравенств будет пересечение решений этих трех неравенств

Ответ. Решение системы неравенств – это множество точек, лежащих в заштрихованной области (рис. 6.22).

Пример 28. Решите систему неравенств

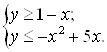
Решение. Решение первого неравенства– это множество точек плоскости, которые лежат выше прямой Решение второго неравенства – это множество точек плоскости внутри параболы . Решением исходной системы неравенств будет пересечение решений этих двух неравенств.

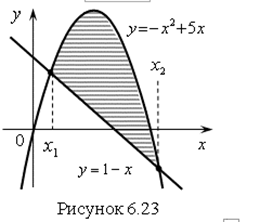
Найдем точки пересечения графиков функций и :

.

Ответ. Решение системы неравенств – это множество точек, лежащих в заштрихованной области (рис. 6.23).

Пример 29. Решите систему неравенств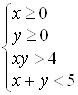

Решение. Решение первого и второго неравенств – это множество точек первого координатного угла (рис. 6.24). Решением третьего неравенства является множество точек, лежащих выше ветви гиперболы при (рис. 6.25).

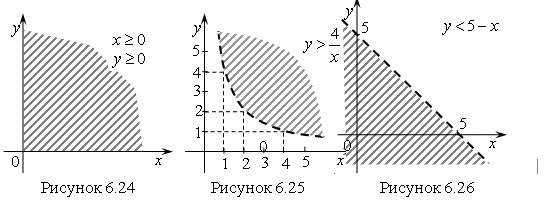
Решением четвертого неравенства является множество точек, лежащих ниже прямой (рис. 6.26).

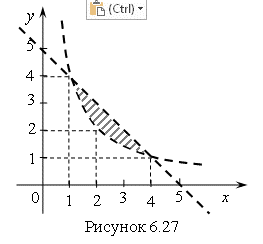
Ответ. Решение системы – это множество точек, лежащих в первой координатной четверти ниже прямой и выше гиперболы (рис. 6.27).

< Предыдущая		Следующая >