083. Иррациональные неравенства

Неравенства, которые содержат переменную под знаком корня, называются Иррациональными.

Например, ; – это иррациональные неравенства.

При решении иррациональных неравенств возможны два случая.

1. .

Это неравенство имеет смысл, если . Поскольку , то . Поэтому обе части неравенства можно возвести в квадрат, т. е. освободиться от иррациональности и получить такую систему неравенств:

.

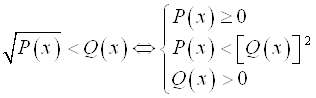Решение данной системы – это решение исходного неравенства.

2. .

Это неравенство имеет смысл, если . Правая часть может принимать положительные значения, отрицательные значения или может быть равна нулю. Поэтому:

.

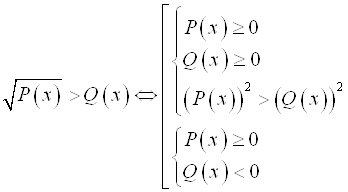Решение иррационального неравенства – это объединение решений двух систем.

Пример 22. Решите неравенство .

Решение.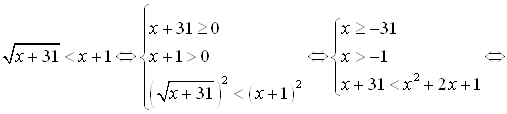

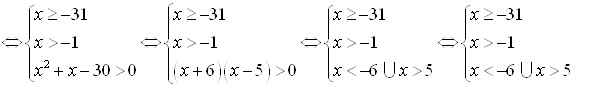
Найдем пересечение решений графически (рис. 6.14):

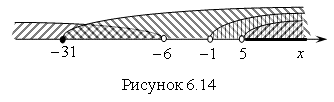
Ответ. .

Пример 23. Решите неравенство .

Решение.

Решение системы (а): 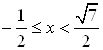(рис. 6.15).

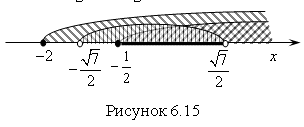
Решение системы (б): (рис. 6.16).

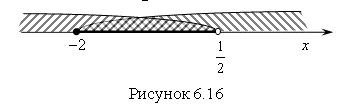
Решение исходного неравенства – это объединение решений (а) и (б):

.

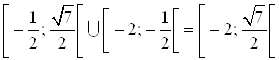Ответ. .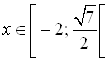

< Предыдущая		Следующая >