082. Неравенства, которые содержат переменную под знаком модуля
При решении неравенств, которые содержат переменную под знаком модуля, используют определение модуля выражения:
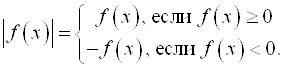
Поэтому неравенство, которое содержит переменную под знаком модуля, равносильно двум системам неравенств, которые можно записать в виде пересечения или объединения двух неравенств.
1. Если ![]() , то
, то 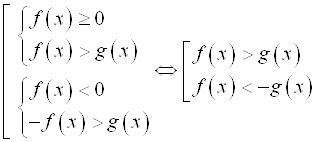 .
.
2. Если ![]() , то
, то 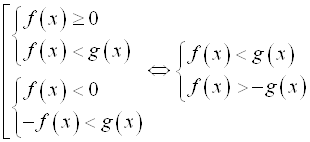 .
.
При решении неравенств, содержащих более одного модуля, также используют метод интервалов.
Пример 15. Решите неравенство ![]() .
.
Решение. По определению модуля имеем: ![]() , поэтому неравенство
, поэтому неравенство ![]() выполняется для любого действительного
выполняется для любого действительного ![]() т. е.
т. е. ![]() .
.
Ответ. ![]() .
.
Пример 16. Решите неравенство ![]() .
.
Решение. 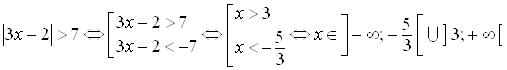 .
.
Ответ. ![]() .
.
Пример 17. Решите неравенство ![]() .
.
Решение. По определению модуля имеем: ![]() поэтому неравенство
поэтому неравенство ![]() решений не имеет.
решений не имеет.
Ответ. Æ.
Пример 18. Решите неравенство ![]() .
.
Решение. 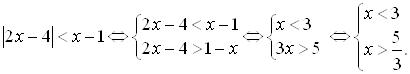
Ответ. 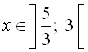 .
.
Пример 19. Решите неравенство ![]() .
.
Решение. Поскольку  , то исходное неравенство можно записать как объединение систем:
, то исходное неравенство можно записать как объединение систем: 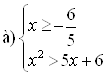 и
и 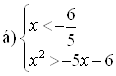 . Решим эти системы и объединим решения а) и б).
. Решим эти системы и объединим решения а) и б).
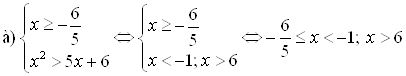 .
.
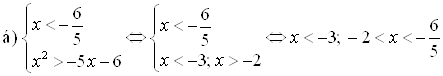 .
.
Ответ. ![]() .
.
Пример 20. Решите неравенство ![]() .
.
Решение. Рассмотрим три случая (раскроем модули на интервалах):
1) 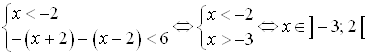 ;
;
2) 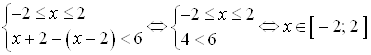 ;
;
3) 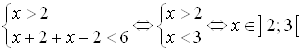 .
.
Объединим полученные решения, получим: ![]() .
.
Ответ. ![]() .
.
Пример 21. Решите неравенство ![]() .
.
Решение. Сделаем замену: ![]()
![]() Получим:
Получим:
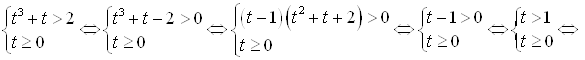
![]() . Тогда:
. Тогда: 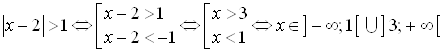 .
.
Ответ. ![]() .
.
| < Предыдущая | Следующая > |
|---|