080. Решение рациональных неравенств методом . интервалов
Рациональным неравенством называется неравенство, в которое входят только рациональные функции (выражения).
Неравенства вида ![]() (или
(или ![]()
![]()
![]()
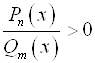 (или
(или 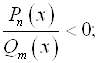
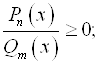
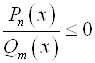 ) обычно решают Методом интервалов. Здесь
) обычно решают Методом интервалов. Здесь ![]() ,
, ![]() ,
, 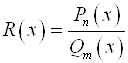 – это рациональные функции (многочлены степеней
– это рациональные функции (многочлены степеней ![]() и
и ![]() , т. е.
, т. е. ![]() ;
;
![]() ).
).
Метод интервалов основывается на важном свойстве рациональной функции: в интервале между двумя соседними критическими точками рациональная функция принимает либо только положительные, либо только отрицательные значения, т. е. сохраняет знак.
Если мы рассматриваем двучлен ![]() тогда точка
тогда точка ![]() делит числовую ось на две части: справа от точки
делит числовую ось на две части: справа от точки ![]() двучлен
двучлен ![]() принимает положительные значения, а слева от точки
принимает положительные значения, а слева от точки ![]() двучлен
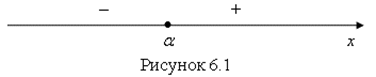
двучлен ![]() принимает отрицательные значения (рис. 6.1).
принимает отрицательные значения (рис. 6.1).
При использовании метода интервалов нужно придерживаться приведенной ниже последовательности действий.
1. Рациональное неравенство приводим к стандартному виду: 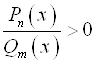 или
или 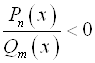 (в случае строгого неравенства),
(в случае строгого неравенства), 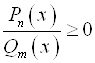 или
или 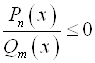 (в случае нестрогого неравенства).
(в случае нестрогого неравенства).
2. Числитель и знаменатель левой части неравенства раскладываем на множители.
3. Находим все критические точки рациональной функции.
4. Разбиваем числовую ось критическими точками на конечное число интервалов.
5. Определяем знак левой части неравенства на каждом интервале, то есть на интервале справа от наибольшего значения критической точки ставим знак "+", на следующем за ним интервале (справа налево) ставим знак "–", потом – знак "+", потом – знак "–" и так далее. Важно помнить, что все вышесказанное имеет место только для многочленов Стандартного вида: когда перед переменной такого многочлена стоит знак "+", то есть, например, ![]() а не
а не ![]() .
.
Если многочлен имеет нестандартный вид ![]() , тогда справа от наибольшей критической точки (числа) не обязательно будет стоять знак "+". Потому, неравенства нестандартного вида можно решать таким образом: найти знак левой части неравенства на любом интервале (не обязательно на последнем интервале справа), а дальше на соседних интервалах будут противоположные знаки.
, тогда справа от наибольшей критической точки (числа) не обязательно будет стоять знак "+". Потому, неравенства нестандартного вида можно решать таким образом: найти знак левой части неравенства на любом интервале (не обязательно на последнем интервале справа), а дальше на соседних интервалах будут противоположные знаки.
6. Записываем решение неравенства в виде интервалов. Тогда множеством всех решений неравенств вида 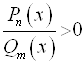 или
или 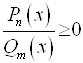 будет объединение всех интервалов, где стоит знак "+". А множест-вом всех решений неравенств вида
будет объединение всех интервалов, где стоит знак "+". А множест-вом всех решений неравенств вида 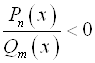 или
или 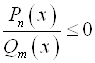 будет объединение всех интервалов, где стоит знак "–".
будет объединение всех интервалов, где стоит знак "–".
При этом, если неравенство нестрогое, то точки, которые соответствуют множителям числителя, отмечаем на числовой оси полными кружками. А точки, которые соответствуют множителям знаменателя, – отмечаем пустыми кружками. Если неравенство строгое, тогда отмечаем все точки пустыми кружками.
При решении неравенств нужно найти ОДЗ неравенства и с его помощью проверить полученные результаты.
ОДЗ неравенства – это множество всех значений переменных, при которых обе части неравенства имеют смысл.
Рассмотрим более подробно использование метода интервалов для решения целых рациональных и дробно-рациональных неравенств с одним неизвестным.
Любое рациональное неравенство ![]() ‑ой степени с одним неизвестным можно привести к стандартному (или каноническому) виду:
‑ой степени с одним неизвестным можно привести к стандартному (или каноническому) виду:
![]() ;
;
![]() ;
;
Или ![]() ;
;
![]() .
.
Рассмотрим Общую схему решения таких неравенств методом интервалов на примере неравенства вида:
![]() .
.
1. Разложим левую часть неравенства на множители:
![]() .
.
2. Запишем множители левой части неравенства с нечетными показателями как множители первой степени. Множители с четными показателями можно опустить (не писать), т. к. они не изменяют знак неравенства. При этом обязательно выпишем те значения ![]() , при которых множители с четными показателями обращаются в нуль. Тогда неравенство примет вид:
, при которых множители с четными показателями обращаются в нуль. Тогда неравенство примет вид:
![]() ;
;
При ![]() оно равносильно неравенству
оно равносильно неравенству ![]() , при
, при ![]() оно равносильно неравенству
оно равносильно неравенству ![]() .
.
3. Отметим на числовой оси числа ![]() (
(![]() – наибольшее число) (рис. 6.2).
– наибольшее число) (рис. 6.2).
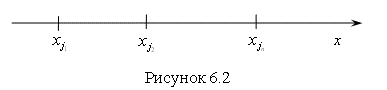
4. Справа от ![]() ставим знак "+" и проводим "кривую знаков" через каждое число
ставим знак "+" и проводим "кривую знаков" через каждое число ![]() (рис. 6.3).
(рис. 6.3).
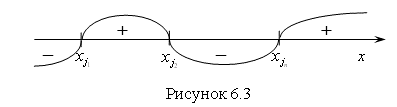
5. Выбираем нужный нам знак (в нашем случае это знак "+") и записываем ответ в виде интервалов (рис. 6.4). При этом исключаем из найденных решений те значения переменных, при которых множители левой части неравенства с четными показателями обращаются в ноль.
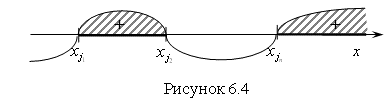
Записываем ответ в виде: ![]() .
.
Пример 6. Решите неравенство ![]() .
.
Решение. ОДЗ: ![]() Найдем нули выражения
Найдем нули выражения ![]() , это будут значения
, это будут значения ![]() или
или ![]() . Отметим найденные значения на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале. Знак исходного неравенства "+", потому решением неравенства будет объединение двух интервалов
. Отметим найденные значения на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале. Знак исходного неравенства "+", потому решением неравенства будет объединение двух интервалов ![]() (рис. 6.5).
(рис. 6.5).
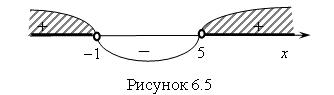
Ответ. ![]() .
.
Пример 7. Решите неравенство ![]() .
.
Решение. Изменяем знак перед переменной ![]() в первой скобке и получаем неравенство
в первой скобке и получаем неравенство ![]() равносильное данному. Разбиваем область допустимых значений на три интервала (в соответствии со значениями в критических точках):
равносильное данному. Разбиваем область допустимых значений на три интервала (в соответствии со значениями в критических точках): ![]()
![]()
![]() . Находим знак на каждом интервале. Знак исходного неравенства "–", поэтому решением неравенства будет объединение двух интервалов
. Находим знак на каждом интервале. Знак исходного неравенства "–", поэтому решением неравенства будет объединение двух интервалов ![]() (рис. 6.6).
(рис. 6.6).
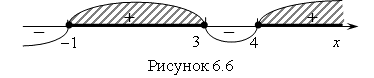
Ответ. ![]() .
.
Пример 8. Решите неравенство ![]() .
.
Решение. Множитель ![]() не изменит знак неравенства
не изменит знак неравенства ![]() при
при ![]() . Тогда исходное неравенство можно записать в виде
. Тогда исходное неравенство можно записать в виде ![]() . Разбиваем область допустимых значений на два интервала (в соответствии со значениями в критических точках)
. Разбиваем область допустимых значений на два интервала (в соответствии со значениями в критических точках) ![]() ,
, ![]() и находим знак на каждом интервале. Знак исходного неравенства "+", поэтому решением неравенства будет объединение двух интервалов
и находим знак на каждом интервале. Знак исходного неравенства "+", поэтому решением неравенства будет объединение двух интервалов ![]() (рис. 6.7)
(рис. 6.7)
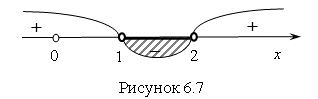
Ответ. ![]() .
.
Пример 9. Решите неравенство ![]() .
.
Решение. 1. Дискриминант квадратного трехчлена ![]() равен:
равен: ![]() первый коэффициент
первый коэффициент ![]() значит, выражение
значит, выражение ![]() при
при ![]() и не изменяет знак неравенства.
и не изменяет знак неравенства.
2. Выражение ![]() при
при ![]() . Следовательно, это выражение также не изменяет знак неравенства.
. Следовательно, это выражение также не изменяет знак неравенства.
3. Изменим знак перед переменной ![]() в первой скобке. Для этого умножим обе части неравенства на
в первой скобке. Для этого умножим обе части неравенства на ![]() и запишем все множители неравенства как множители в первой степени. Выражение
и запишем все множители неравенства как множители в первой степени. Выражение ![]() не изменяет знак неравенства, потому его можно не записывать, однако нужно проверить, является ли точка
не изменяет знак неравенства, потому его можно не записывать, однако нужно проверить, является ли точка ![]() решением исходного неравенства. Получим:
решением исходного неравенства. Получим: ![]() (рис. 6.8).
(рис. 6.8).
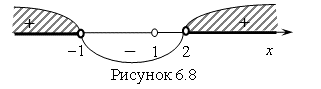
Точка ![]() Не принадлежит области решений исходного неравенства, поэтому эта точка не будет решением неравенства.
Не принадлежит области решений исходного неравенства, поэтому эта точка не будет решением неравенства.
Ответ. ![]() .
.
При решении дробно-рациональных неравенств используют следующие утверждения:
1. Неравенства 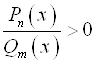 и
и 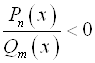 равносильны неравенствам
равносильны неравенствам ![]() и
и ![]() соответственно.
соответственно.
2. Неравенства 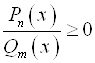 и
и 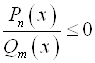 равносильны системам неравенств
равносильны системам неравенств 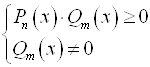 и
и 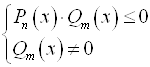 соответственно.
соответственно.
Таким образом, решение дробно-рациональных неравенств, как правило, сводится к решению целых рациональных неравенств.
Пример 10. Решите неравенство 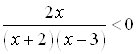 .
.
Решение. ОДЗ неравенства: ![]()
![]() Запишем исходное неравенство в виде
Запишем исходное неравенство в виде ![]() . Нули этого неравенства:
. Нули этого неравенства: ![]()
![]()
![]() Обозначим эти точки на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале (рис. 6.9).
Обозначим эти точки на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале (рис. 6.9).
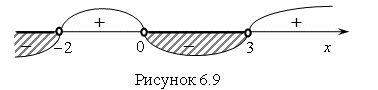
Ответ. ![]() .
.
Пример 11. Решите неравенство 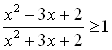 .
.
Решение. ОДЗ неравенства: ![]()
![]() Выполним тождественные преобразования выражения:
Выполним тождественные преобразования выражения: 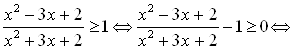
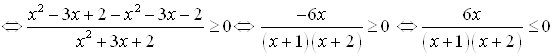 .
.
Запишем исходное неравенство в виде: ![]()
Нули этого неравенства: ![]()
![]()
![]() Обозначим эти точки на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале (рис. 6.10).
Обозначим эти точки на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале (рис. 6.10).
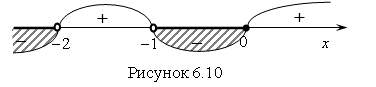
Ответ. ![]() .
.
Метод интервалов удобно использовать и для решения неравенств вида: ![]() а также
а также 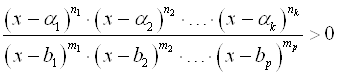 .
.
Пример 12. Решите неравенство 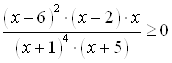 .
.
Решение. В выражениях ![]() и
и ![]() показатели степени – это четные числа, поэтому
показатели степени – это четные числа, поэтому ![]() ;
; ![]() при
при ![]() . Следовательно, эти выражения не изменяют знак неравенства (рис. 6.11). Запишем исходное неравенство в виде равносильного неравенства:
. Следовательно, эти выражения не изменяют знак неравенства (рис. 6.11). Запишем исходное неравенство в виде равносильного неравенства: ![]() .
.
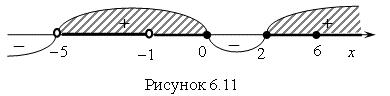
Значения ![]() и
и ![]() Не могут быть решением неравенства, поэтому их нужно исключить из интервала решений.
Не могут быть решением неравенства, поэтому их нужно исключить из интервала решений.
Ответ. ![]() .
.
| < Предыдущая | Следующая > |
|---|