079. Линейные и квадратные неравенства
Линейными неравенствами с одной переменной называются неравенства вида 
; 
; 
; 
.
Пример 1. Решите неравенство 
.
Решение. Раскроем скобки и сделаем необходимые преобразования: 
.
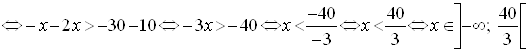Решением исходного неравенства будет открытый интервал от "минус" бесконечности до сорока третьих.
Ответ.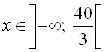 
.
Пример 2. Решите неравенство 
.
Решение. Умножим обе части неравенства на 3 и сделает преобразования:
.
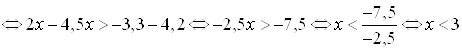Ответ. 
.
Неравенства вида 
или 
, где 
называются Квадратными неравенствами или неравенствами второй степени.
Если есть неравенство, где 
, то можно умножить обе части неравенства на 
и изменить знак неравенства на противоположный. Тогда получим неравенство, равносильное данному, где 
.
На основании вышесказанного, рассмотрим только решение неравенств вида 
, и , где . При решении квадратных неравенств учитывают свойства квадратной функции, графиком которой является парабола.
Рассмотрим три случая.
I. Если 
, , то неравенство верно при всех 
(парабола расположена выше оси 
), а неравенство не имеет решений (парабола расположена ниже оси ), т. е. 
.
Пример 3. Решите неравенство 
.
Решение. Найдем значение дискриминанта данного квадратного уравнения: 
Так как 
, то выражение 
имеет положительные значения на всей числовой оси, т. е. 
.
Ответ. 
.
II. А) Если 
, и тогда это неравенство можно записать в виде:
.
(Парабола пересекает ось в двух точках 
и 
, ее ветви направлены вверх. Решением данного неравенства будут интервалы, на которых парабола расположена выше оси ).
Б) Если , и 
тогда это неравенство можно записать в виде:
(Парабола пересекает ось в двух точках и , ее ветви направлены вверх. Решением данного неравенства будут интервалы, на которых парабола расположена ниже оси ).
Пример 4. Решите неравенство 
.
Решение. Рассмотрим квадратный трехчлен 
у которого 
; 
, тогда его корни 
Представим левую часть неравенства в виде произведения 
Ответ. 
III. А) Если 
, и тогда это неравенство можно записать в виде:
.
(Парабола имеет с осью одну общую точку 
, ее ветви направлены вверх. Решением данного неравенства будет вся числовая ось , за исключением общей точки ).
Б) Если , и тогда это неравенство можно записать в виде:
.
(Парабола имеет с осью одну общую точку , ее ветви направлены вверх. Так как левая часть неравенства может принимать только неотрицательные значения, то решений нет).
Пример 5. Решите неравенство 
.
Решение. Умножим обе части неравенства на 
получим: 
Тогда: 
Поэтому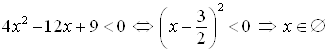 
.
Ответ. 
.
| < Предыдущая | Следующая > |
|---|
