078. Неравенства. Основные теоремы равносильности неравенств
Выражения, соединенные знаками больше (
), меньше (
), больше или равно (
), меньше или равно (
) называются Неравенствами.
; 
; 
; 
– это неравенства.
Решения неравенства – это такие значения переменной, при которых данное неравенство будет верным числовым неравенством.
Решить неравенство – это значит найти все его решения или доказать что их нет.
Два неравенства с одной переменной называются Равносильными (эквивалентными), если решения этих неравенств совпадают.
При решении неравенств используют теоремы о равносильности неравенств. При этом области определения полученного и исходного неравенств совпадают.
Теорема 1. Если к обеим частям неравенства прибавить (вычесть) одно и то же число (выражение), то получим неравенство, равносильное данному.
.
Например, 
.
Теорема 2. Если любое слагаемое неравенства перенести в другую часть с противоположным знаком, то получим неравенство, равносильное данному.
.
Например, 
.
Теорема 3. Если обе части неравенства умножить (разделить) на одно и то же положительное число (выражение), то получим неравенство, равносильное данному.
.
Например,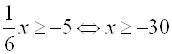 
.
Теорема 4. Если обе части неравенства умножить (разделить) на одно и то же отрицательное число (выражение) и изменить знак неравенства на противоположный, то получим неравенство, равносильное данному.
.
Например, 
.
| < Предыдущая | Следующая > |
|---|
