072. Основные тригонометрические функции
Основными тригонометрическими функциями являются: ![]()
![]()
![]()
![]() .
.
Свойства и график функции ![]()
1. Область определения: ![]() или
или ![]() .
.
2. Область значений: ![]() или
или ![]() .
.
3. Функция нечетная, так как ![]() . График функции симметричен относительно начала координат
. График функции симметричен относительно начала координат ![]() .
.
4. Функция периодическая; основной период ![]() .
.
5. Нули функции: ![]() при
при ![]() .
.
6. Функция возрастает на интервалах 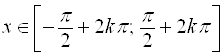 и убывает на интервалах
и убывает на интервалах 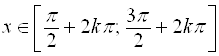 ,
, ![]() .
.
7. Экстремумы функции: а) ![]() при
при ![]() ;
;
Б) ![]() при
при ![]() .
.
8. Функция не имеет асимптот.
9. ![]() при
при ![]() ;
; ![]() при
при ![]() .
.
10. Функция ограниченная: ![]() .
.
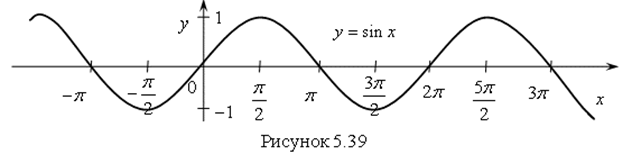
График функции ![]() изображен на рисунке 5.39. Он называется Синусоидой.
изображен на рисунке 5.39. Он называется Синусоидой.
Свойства и график функции ![]()
1. Область определения: ![]() или
или ![]() .
.
2. Область значений: ![]() или
или ![]() .
.
3. Функция четная, так как ![]() . График функции симметричен относительно оси
. График функции симметричен относительно оси ![]() .
.
4. Функция периодическая; основной период ![]() .
.
5. Нули функции: ![]() при
при ![]() .
.
6. Функция возрастает на промежутках ![]() ,
, ![]() и убывает на промежутках
и убывает на промежутках ![]() ,
, ![]() .
.
7. Экстремумы функции: а) ![]() при
при ![]() ;
;
Б) ![]() при
при ![]() .
.
8. Функция не имеет асимптот.
9. ![]() при
при ![]() ;
; ![]() при
при ![]() .
.
10. Функция ограниченная: ![]() .
.
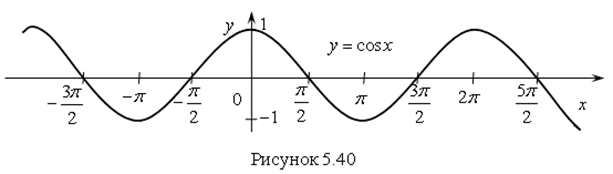
График функции ![]() изображен на рис. 5.40. Он называется Косинусоидой.
изображен на рис. 5.40. Он называется Косинусоидой.
Свойства и график функции ![]()
1. Область определения: 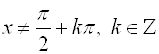 или
или
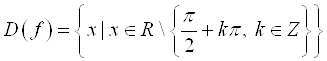 .
.
2. Область значений: ![]() или
или ![]() .
.
3. Функция нечетная, так как ![]() . График функции симметричен относительно начала координат.
. График функции симметричен относительно начала координат.
4. Функция периодическая; основной период ![]() .
.
5. Нули функции: 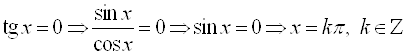 .
.
6. Функция возрастает на промежутках 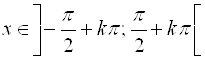 ,
, ![]() .
.
7. Функция не имеет экстремумов.
8. Прямые 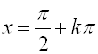 ,
, ![]() , являются вертикальными асимптотами.
, являются вертикальными асимптотами.
9. ![]() при
при 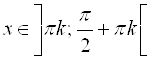 ;
; ![]() при
при 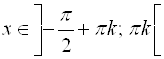 .
.
10. Функция неограниченная.
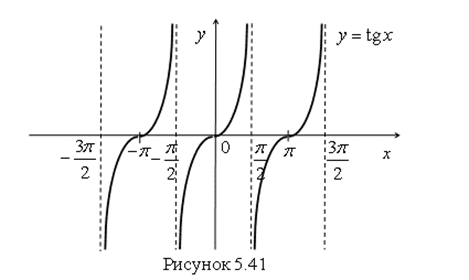
График функции ![]() изображен на рис. 5.41. Он называется Тангенсоидой.
изображен на рис. 5.41. Он называется Тангенсоидой.
Свойства и график функции ![]()
1. Область определения: ![]() или
или
![]() .
.
2. Область значений: ![]() или
или ![]() .
.
3. Функция нечетная, так как ![]() . График функции симметричен относительно начала координат.
. График функции симметричен относительно начала координат.
4. Функция периодическая; основной период ![]() .
.
5. Нули функции:
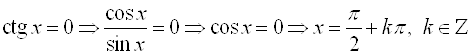 .
.
6. Функция убывает на промежутках ![]() ,
, ![]() .
.
7. Функция не имеет экстремумов.
8. Прямые ![]() ,
, ![]() , являются вертикальными асимптотами.
, являются вертикальными асимптотами.
9. ![]() при
при 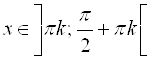 ;
; ![]() при
при 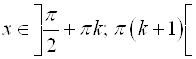 .
.
10. Функция неограниченная.
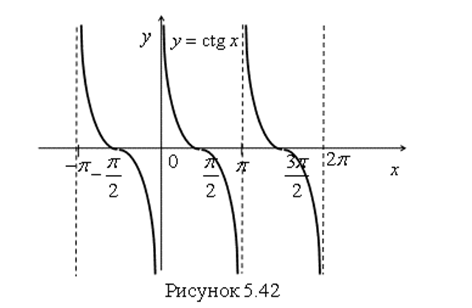
График функции ![]() изображен на рис. 5.42. Он называется Котангенсоидой.
изображен на рис. 5.42. Он называется Котангенсоидой.
| < Предыдущая | Следующая > |
|---|