073. Обратные тригонометрические функции
Функции, обратные функциям ![]() ,
, ![]() ,
, ![]() ,
, ![]() на соответствующих интервалах, называются Обратными тригонометрическими функциями. Они обозначаются:
на соответствующих интервалах, называются Обратными тригонометрическими функциями. Они обозначаются: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Тригонометрические функции ![]() и
и ![]() не являются монотонными во всей области их определения. Поэтому для построения обратных тригонометрических функций выделяют интервалы монотонности.
не являются монотонными во всей области их определения. Поэтому для построения обратных тригонометрических функций выделяют интервалы монотонности.
Функция ![]()
Функция ![]() возрастает на отрезке (интервале)
возрастает на отрезке (интервале) 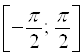 и принимает все значения от
и принимает все значения от ![]() до
до ![]() . Значит, для функции
. Значит, для функции ![]() ,
, ![]() , существует обратная функция. Эту функцию обозначают
, существует обратная функция. Эту функцию обозначают ![]() (читается "арксинус икс").
(читается "арксинус икс").
Арксинус числа ![]() – это такое число
– это такое число ![]() из отрезка
из отрезка 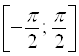 , синус которого равен
, синус которого равен ![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
Например: ![]() (так как
(так как ![]() ;
; ![]() );
); ![]() ;
; ![]() ;
; ![]() ;
; 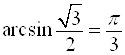 .
.
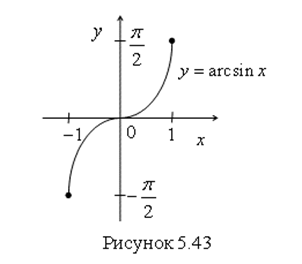
График функции ![]() изображен на рис. 5.43. Этот график симметричен графику функции
изображен на рис. 5.43. Этот график симметричен графику функции ![]() ,
, 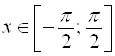 относительно прямой
относительно прямой ![]() .
.
Основные свойства функции ![]()
1. Область определения: ![]() .
.
2. Множество значений: 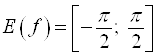 .
.
3. Функция нечетная, так как ![]() .
.
4. Нули функции: ![]() при
при ![]() .
.
5. ![]() при
при ![]() и
и ![]() при
при ![]() .
.
6. Функция возрастает на всей области определения.
7. Функция не имеет экстремумов.
8. Функция не имеет асимптот.
9. ![]() при
при ![]() .
.
10. Функция непериодическая.
При рассмотрении обратной функции ![]() на отрезке
на отрезке 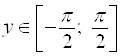 значение
значение ![]() называют главным значением и обозна-чают
называют главным значением и обозна-чают ![]() . Другие значения
. Другие значения ![]() выражаются через его главное значение формулой:
выражаются через его главное значение формулой: ![]() .
.
Функция ![]()
Функция ![]() убывает на отрезке
убывает на отрезке ![]() и принимает все значения от
и принимает все значения от ![]() до
до ![]() . Значит, для функции
. Значит, для функции ![]() ,
, ![]() , существует обратная функция. Эту функцию обозначают
, существует обратная функция. Эту функцию обозначают ![]() (читается "арккосинус икс").
(читается "арккосинус икс").
Арккосинус числа ![]() – это такое число
– это такое число ![]() из отрезка
из отрезка ![]() , косинус которого равен
, косинус которого равен ![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
Например, 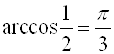 (так как
(так как 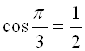 ;
; 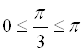 );
); ![]() ;
; ![]() ;
; 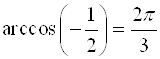 .
.
Отметим, что имеет место следующее важное тождество:
![]() .
.
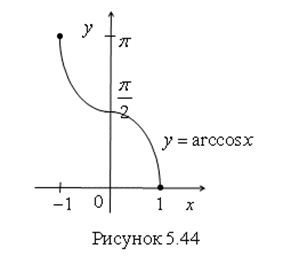
В его справедливости можно убедиться с помощью графика функции ![]() (рис. 5.44). Этот график симметричен графику функции
(рис. 5.44). Этот график симметричен графику функции ![]() ,
, ![]() относительно прямой
относительно прямой ![]() .
.
Основные свойства функции ![]()
1. Область определения: ![]() .
.
2. Множество значений: ![]() .
.
3. Функция общего вида: ![]() .
.
4. Нули функции: ![]() при
при ![]() .
.
5. ![]() при
при ![]() .
.
6. Функция убывающая.
7. Функция не имеет экстремумов.
8. Функция не имеет асимптот.
9. ![]() при
при ![]() .
.
10. Функция непериодическая.
При рассмотрении обратной функции ![]() на отрезке
на отрезке ![]() значение
значение ![]() называют главным значением и обозначают
называют главным значением и обозначают ![]() . Другие значения
. Другие значения ![]() выражаются через его главное значение формулой:
выражаются через его главное значение формулой: ![]() .
.
Функция ![]()
Функция ![]() возрастает на отрезке
возрастает на отрезке 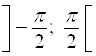 и принимает на нем все числовые значения, так как
и принимает на нем все числовые значения, так как ![]() . Значит, на указанном интервале для функции
. Значит, на указанном интервале для функции ![]() существует обратная функция. Эту функцию обозначают
существует обратная функция. Эту функцию обозначают ![]() (читается "арктангенс икс").
(читается "арктангенс икс").
Арктангенс числа ![]() – это такое число
– это такое число ![]() из отрезка
из отрезка 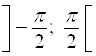 , тангенс которого равен
, тангенс которого равен ![]() :
:
![]() ,
, 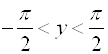 ,
, ![]() .
.
Например, 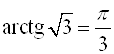 (так как
(так как 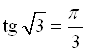 ;
; 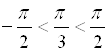 );
); ![]() ;
; 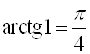 ;
; 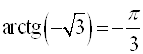 ;
; 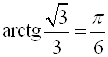 ;
; 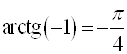 .
.
График функции ![]() изображен на рис. 5.45. Этот график симметричен графику функции
изображен на рис. 5.45. Этот график симметричен графику функции ![]() ,
, 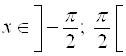 относительно прямой
относительно прямой ![]() . Прямые
. Прямые 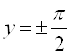 являются горизонтальными асимптотами графика функции
являются горизонтальными асимптотами графика функции ![]() .
.
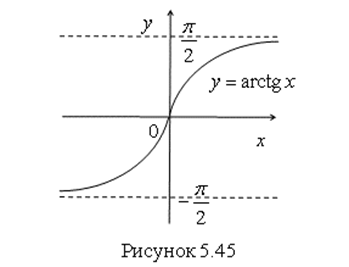
Основные свойства функции ![]()
1. Область определения: ![]() .
.
2. Множество значений: 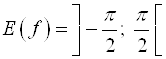 .
.
3. Функция нечетная: ![]() .
.
4. Нули функции: ![]() при
при ![]() .
.
5. ![]() при
при ![]() и
и ![]() при
при ![]() .
.
6. Функция возрастающая.
7. Функция не имеет экстремумов.
8. Асимптоты функции: 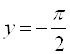 и
и 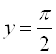 .
.
9. ![]() при
при ![]() .
.
10. Функция непериодическая.
Функция ![]() определена для
определена для ![]() и многозначна. Значение
и многозначна. Значение ![]() называют Главным значением и обозначают
называют Главным значением и обозначают ![]() . Другие значения
. Другие значения ![]() выражаются через его главное значение формулой:
выражаются через его главное значение формулой:
![]() .
.
Функция ![]()
Функция ![]() убывает на отрезке
убывает на отрезке ![]() и принимает на нем все числовые значения, так как
и принимает на нем все числовые значения, так как ![]() . Значит, на указанном интервале для функции
. Значит, на указанном интервале для функции ![]() существует обратная функция. Эту функцию обозначают
существует обратная функция. Эту функцию обозначают ![]() (читается "арккотангенс икс").
(читается "арккотангенс икс").
Арккотангенс числа ![]() – это такое число
– это такое число ![]() из отрезка
из отрезка ![]() , котангенс которого равен
, котангенс которого равен ![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
Например, 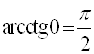 (так как
(так как 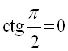 ;
; 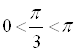 );
); 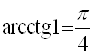 ;
; 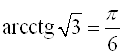 ;
; 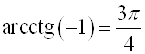 ;
; 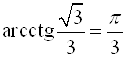 ;
; 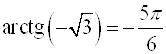 .
.
Отметим, что имеет место следующее важное тождество:
![]() .
.
График функции ![]() изображен на рис. 5.46.
изображен на рис. 5.46.
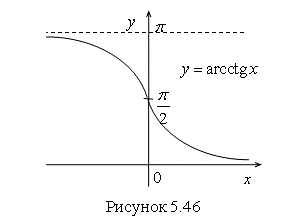
График функции ![]() симметричен графику функции
симметричен графику функции ![]() ,
, ![]() относительно прямой
относительно прямой ![]() . Прямые
. Прямые ![]() и
и ![]() являются горизонтальными асимптотами графика функции
являются горизонтальными асимптотами графика функции ![]() .
.
Основные свойства функции ![]()
1. Область определения: ![]() .
.
2. Множество значений: ![]() .
.
3. Функция общего вида: ![]() .
.
4. Нулей функции нет.
5. ![]() при
при ![]() .
.
6. Функция убывающая.
7. Функция не имеет экстремумов.
8. Асимптоты функции: ![]() и
и ![]() .
.
9. ![]() при
при ![]() .
.
10. Функция непериодическая.
Функция ![]() определена для
определена для ![]() и многозначна. Значение
и многозначна. Значение ![]() называют главным значением и обозначают
называют главным значением и обозначают ![]() . Другие значения
. Другие значения ![]() выражаются через его главное значение формулой:
выражаются через его главное значение формулой: ![]() .
.
| < Предыдущая | Следующая > |
|---|