071. Логарифмическая функция

Функция, заданная формулой (, ) называется Логарифмической.

Читаем так: "Игрек равен логарифму икс по основанию ".

Логарифмом положительного числа по основанию называется показатель степени, в которую нужно возвести число , чтобы получить число . Из определения логарифм мы получаем: .

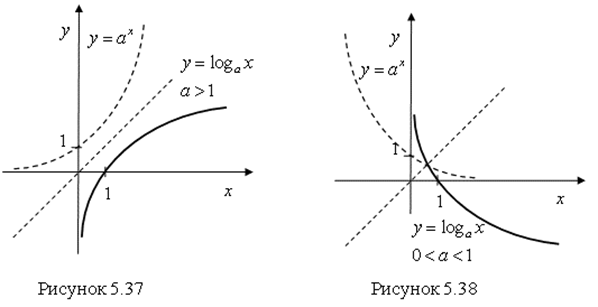
Логарифмическая функция является обратной для показательной функции , графики этих функций симметричны относительно прямой (рис. 5.37, 5.38).

Рассмотрим свойства и график функции при и .

Свойства функции
При	При
1. Область определения функции: .	1. Область определения функции: .
2. Область значений функции: .	2. Область значений функции: .
3. Функция ни четная, ни нечетная, т. е. общего вида.	3. Функция общего вида.
4. Функция возрастает при .	4. Функция убывает при .
5. Нули функции при .	5. Нули функции при .
6.  при и при .	6.  при и при .
7. Функция не имеет экстремумов.	7. Функция не имеет экстремумов.
8. Вертикальная асимптота	8. Вертикальная асимптота

< Предыдущая		Следующая >