066. Дробно-рациональная функция
Дробно-рациональная функция ![]() определяется отношением двух многочленов и имеет вид:
определяется отношением двух многочленов и имеет вид:
 .
.
Областью определения такой функции будут все значения ![]() кроме тех, в которых знаменатель функции обращается в нуль. Значения
кроме тех, в которых знаменатель функции обращается в нуль. Значения ![]()
![]() , в которых
, в которых ![]() называются Точками разрыва функции.
называются Точками разрыва функции.
Дробно-рациональной функцией является и функция 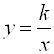 (обратная пропорциональность).
(обратная пропорциональность).
Функция 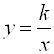 , если
, если ![]() , имеет вид
, имеет вид 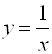 (рис. 5.24), а если
(рис. 5.24), а если ![]() , имеет вид
, имеет вид 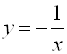 (рис. 5.25). Рассмотрим данные функции более подробно.
(рис. 5.25). Рассмотрим данные функции более подробно.

|
Свойства функции |
Свойства функции |
|
1. ( |
1. ( |
|
2. |
2. |
|
3. Функция не имеет нулей. График функции не пересекает ось |
3. Функция не имеет нулей. График функции не пересекает ось |
|
4. |
4. |
|
5. Функция монотонно убывает в каждом из интервалов
|
5. Функция монотонно возраста-ет в каждом из интервалов
|
|
6. Функция не имеет экстремумов. |
6. Функция не имеет экстремумов. |
|
7. Функция нечетная ( |
7. Функция нечетная ( |
|
8. График функции не пересекает оси координат. Оси |
8. График функции не пересекает оси координат. Оси |
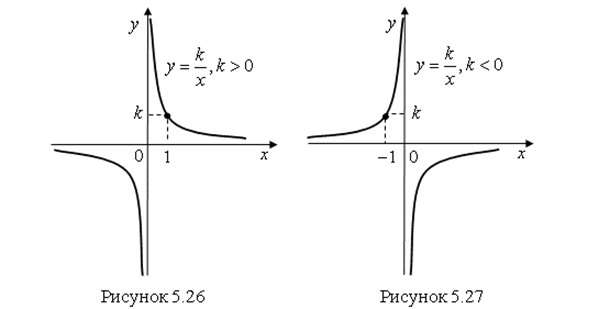
Графиком функции ![]() есть Гипербола. Ординаты ее графика в
есть Гипербола. Ординаты ее графика в ![]() раз по модулю больше ординат графика функции
раз по модулю больше ординат графика функции 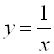 (рис. 5.26) или
(рис. 5.26) или 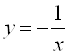 (рис. 5.27).
(рис. 5.27).
Отношение двух линейных функций представляет собой дробно-линейную функцию ![]() .
.
Дробно-линейную функцию ![]() , где
, где ![]() , можно записать в виде:
, можно записать в виде: ![]() , где
, где 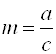 ,
,  и
и 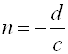 . Получим эту формулу преобразованием формулы:
. Получим эту формулу преобразованием формулы: 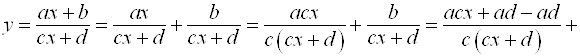
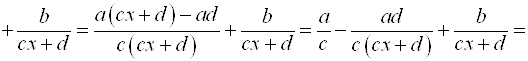
 .
.
Полученная формула позволяет построить график функции 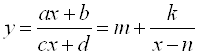 сдвигом графика
сдвигом графика 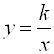 на
на ![]() единиц вдоль оси
единиц вдоль оси ![]() и на
и на ![]() единиц вдоль оси
единиц вдоль оси ![]() (рис. 5.28).
(рис. 5.28).

Уравнение вертикальной асимптоты имеет вид: ![]() ,
,
а уравнение горизонтальной асимптоты имеет вид: ![]() .
.
Пример 2. Построить график функции ![]() .
.
Решение. В дробно-линейной функции ![]() коэффициенты
коэффициенты ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Вычислим значения ![]() ,
, ![]() и
и ![]() . Запишем преобразованную формулу функции:
. Запишем преобразованную формулу функции: ![]() .
.
Эту же формулу можно получить преобразованием заданной функции:

![]() .
.
Построим график функций ![]() (рис. 5.29) и
(рис. 5.29) и ![]() (рис. 5.30).
(рис. 5.30).
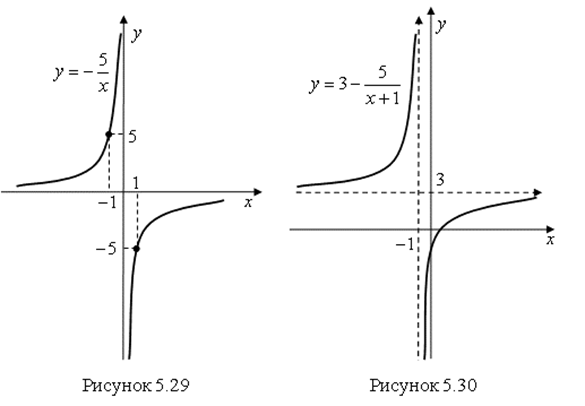
Ответ. График функции ![]() получен сдвигом графика функции
получен сдвигом графика функции ![]() на 1 единицу вдоль оси
на 1 единицу вдоль оси ![]() влево и на 3 единицы вдоль оси
влево и на 3 единицы вдоль оси ![]() вверх.
вверх.
| < Предыдущая | Следующая > |
|---|