065. Степенная функция
Если в выражении для целой рациональной функции ![]() положить, что
положить, что ![]() и
и ![]() , то получим
, то получим ![]() .
.
Функция вида ![]() , где
, где ![]() называется Степенной функцией.
называется Степенной функцией.
При ![]() мы имеем
мы имеем ![]() – Прямую пропорциональность (
– Прямую пропорциональность (![]() – коэффициент прямой пропорциональности), а при
– коэффициент прямой пропорциональности), а при ![]() ,
, 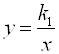 – это Обратная пропорциональность (
– это Обратная пропорциональность (![]() – коэффициент обратной пропорциональности).
– коэффициент обратной пропорциональности).
Если в формуле ![]() положить
положить ![]() , то график функции
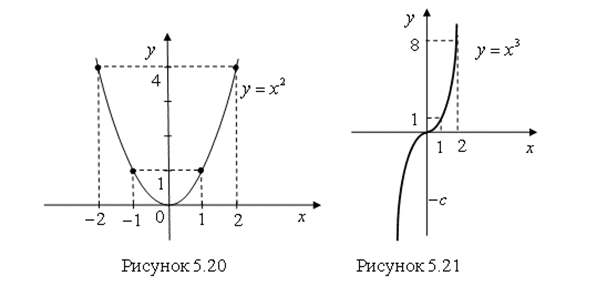
, то график функции ![]() есть Парабола (рис. 5.20), а при
есть Парабола (рис. 5.20), а при ![]() график функции
график функции ![]() это Кубическая парабола (рис. 5.21).
это Кубическая парабола (рис. 5.21).
|
Свойства функции |
Свойства функции |
|
1. |
1. |
|
2. |
2. |
|
3. Функция имеет один нуль ( |
3. Функция имеет один нуль ( |
|
4. |
4. |
|
5. Функция убывает на интерва-ле |
5. Функция монотонно возрастает во всей области определения. |
|
6. Функция имеет минимум при |
6. Функция не имеет экстремумов. |
|
7. Функция четная ( |
7. Функция нечетная ( |
|
8. График функции не имеет асимптот. |
8. График функции не имеет асимптот. |
Рассмотрим еще одну целую рациональную функцию ![]() , которую можно получить из многочлена
, которую можно получить из многочлена ![]() -ой степени при
-ой степени при ![]() .
.
Функция вида ![]() , где
, где ![]() , называется Квадратичной функцией. Областью определения этой функции есть вся числовая ось,
, называется Квадратичной функцией. Областью определения этой функции есть вся числовая ось, ![]() .
.
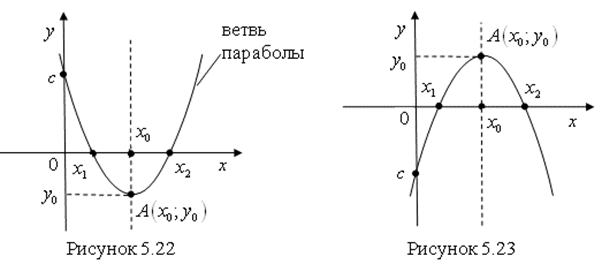
Графиком функции является парабола. Ветви параболы направлены вверх при ![]() (рис. 5.22) и вниз при
(рис. 5.22) и вниз при ![]() (рис. 5.23).
(рис. 5.23).
Осью симметрии параболы есть прямая  .
.
Координаты вершины параболы находят по формулам:
 ,
, 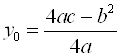 .
.
Для построения графика функции преобразуем выражение:

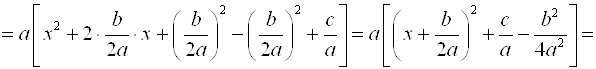
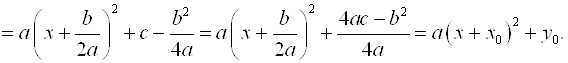
Такое преобразование называется выделением полного квадрата.
| < Предыдущая | Следующая > |
|---|