064. Свойства линейной функции y=kx+b

1. Область определения линейной функции – это вся числовая ось: .

2. Область значений этой функции: .

3. Функция монотонно возрастает при (рис. 5.13) и монотонно убывает при (рис. 5.14).

4. Нули функции: при .

5. Если , то при , при .

Если , то при , при .

6. Функция общего вида.

7. Функция не имеет экстремумов.

8. График функции не имеет асимптот.

Если в формуле положить , то получим – это прямая, которая параллельна оси (рис. 5.15). Это график постоянной функции.

Если в формуле положить и , то получим – прямая совпадает с осью (рис. 5.16).

Если в формуле положить что , а , то получим . Эта функция называется Прямой пропорциональностью. График функции – это прямая линия, которая проходит через начало координат (рис. 5.17).

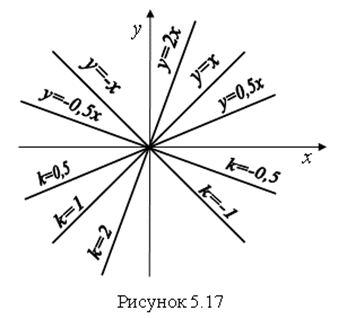
Рассмотрим свойства еще двух функций и . Эти функции получаются из формулы при .

Графиками функций (рис. 5.18) и (рис. 5.19) будут прямые линии, которые проходят через начало координат.

Свойства функции	Свойства функции
1. .	1. .
2. .	2. .
3. Нуль функции: при .	3. Нуль функции: при .
4.  при ; при .	4.  при ; при .
5. Функция возрастает на всей области определения.	5. Функция убывает на всей области определения.
6. Функция нечетная . График функции симметричен относительно начала координат.	6. Функция нечетная . График функции симметричен относительно начала координат.
7. Функция не имеет экстремумов.	7. Функция не имеет экстремумов.
8. График функции не имеет асимптот.	8. График функции не имеет асимптот.

< Предыдущая		Следующая >