063. Линейная функция
Рассмотрим целую рациональную функцию, которая задана многочленом ![]() .
.
При ![]() в правой части равенства будет многочлен первой степени
в правой части равенства будет многочлен первой степени ![]() . Это Линейная функция. Формулу этой функции чаще всего записывают в виде
. Это Линейная функция. Формулу этой функции чаще всего записывают в виде ![]() . Здесь
. Здесь ![]() и
и ![]() – это некоторые фиксированные числа.
– это некоторые фиксированные числа.
Графиком линейной функции будет прямая линия. Чтобы построить график этой функции достаточно знать координаты двух точек в системе координат ![]() .
.
Возьмем точку ![]() и точку
и точку ![]() и из формулы
и из формулы ![]() получим, что
получим, что ![]() и
и 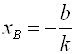 ,
, ![]() .
.
На координатных осях ![]() и
и ![]() отложим значения координат точек
отложим значения координат точек ![]() и
и 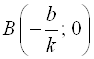 . Соединим прямой линией точки
. Соединим прямой линией точки ![]() и
и ![]() . Полученная прямая
. Полученная прямая ![]() Есть график функции
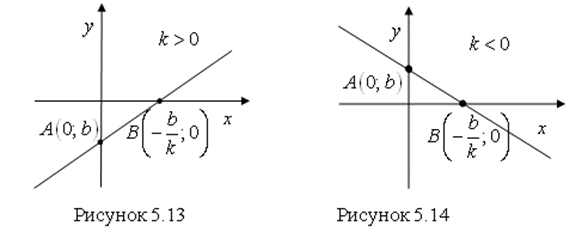
Есть график функции ![]() ( . 5.13, если
( . 5.13, если ![]() и рис. 5.14, если
и рис. 5.14, если ![]() ).
).
| < Предыдущая | Следующая > |
|---|