058. Интервалы знакопостоянства, нули и экстремумы функции. Асимптоты

Значения переменной , при которых функция равна нулю, называются Нулями (корнями) функции.

Например, для функции (рис. 5.8) нулями функции будут точки , .

При переходе через ноль функция меняет знак. Числовые интервалы, на которых функция сохраняет знак, называются Интервалами знакопостоянства.

Например, Интервалами положительности для функции будут интервалы , а Интервалами отрицательности будут интервалы (рис. 5.8)..

Значение переменной из области определения функции называется Точкой минимума, если есть такая ‑окрестность этой точки , что для всех выполняется неравенство . Значение функции в этой точке называется Минимальным значением функции (Минимумом функции).

Например, для функции точками минимума будут точки 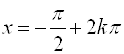, . Минимальное значение функции (рис. 5.8).

Значение переменной из области определения функции называется Точкой максимума, если есть такая ‑окрестность этой точки , что для всех выполняется неравенство . Значение функции в этой точке называется Максимальным значением функции (Максимумом функции).

Например, для функции точками максимума будут точки 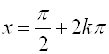, . Максимальное значение функции (рис. 5.8).

Точки максимума и минимума называются Точками экстремума. Значения функции в точках максимума и минимума называются Экстремумами функции (максимумом и минимумом функции).

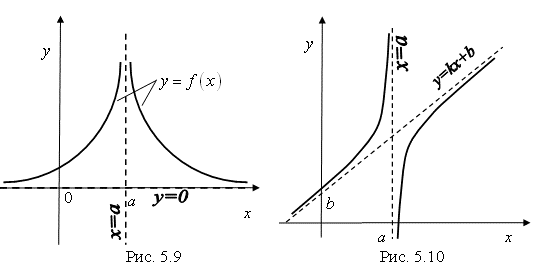
Асимптота графика функции – это прямая линия, к которой неограниченно приближается кривая при удалении ее от начала координат в бесконечность.

Асимптоты бывают: вертикальные () (рис. 5.9, 5.10), горизонтальные () (рис. 5.9) и наклонные () (рис. 5.10).