056. Четность и нечетность функции

Числовое множество называется Симметричным, если для всех , принадлежащих этому множеству, их противоположные значения также принадлежат этому множеству.

Например, если , то и .

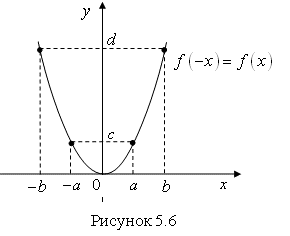
Функция , определенная на симметричном множестве , называется Четной, (рис. 5.6), если для выполняется равенство .

Например, – четная функция, так как и . У четной функции для противоположных значений "" (, ) значение "" одинаковое. График такой функции симметричен относительно оси Оу.

Функция , определенная на симметричном множестве , называется Нечетной, (рис. 5.7), если для выполняется равенство .

Например, – нечетная функция, так как и .

График нечетной функции симметричен относительно Начала координат.

Функция есть Четная или Нечетная, если:

1. область ее определения симметрична;

2. выполняется одно из равенств .

Функции, которые не являются ни четными, ни нечетными, называются функциями Общего вида.

Например, – функция общего вида, так как ; – функция общего вида, так как область ее определения несимметрична ().

< Предыдущая		Следующая >