050. Симметричные системы уравнений

Выражение называется Симметричным, если при замене на или на оно не изменяется. Например, – это симметричные выражения.

Выражения и называют Основными симметричными многочленами с двумя переменными.

Все симметричные выражения с двумя переменными можно выразить через основные симметричные многочлены, такие как:

; ;

Симметричная система уравнений – это такая система, все уравнения которой симметричны.

Решать симметричные системы можно с помощью замены переменных, где новые переменные – это основные симметричные многочлены.

Пример 54. Решите систему .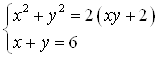

Решение. Сделаем замену: Преобразуем многочлен , получим .

Получим новую систему относительно и :

.

Поэтому,

Ответ. .

Пример 55. Решите систему .

Решение. Сделаем преобразования:

А) ;

Б) .

Сделаем замену: Получим новую систему:

.

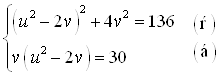Из уравнения (б) последней системы: . Подставляем в уравнение (а), получаем: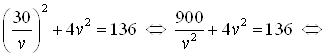

Из уравнения (б): .

Подставим найденные значения , получим:

Если ;

Если ;

Если или , то действительных значений не существует.

Тогда получаем: ; ; ; .

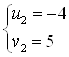Исходная система равносильна совокупности четырех систем:

; ; ; .

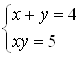Первая и вторая системы решений не имеют. Решениями третьей системы будут: ; . Решения четвертой системы: ; .

Ответ. .

< Предыдущая		Следующая >