049. Однородные системы уравнений

Система уравнений называется Однородной, если левые части ее уравнений – это однородные многочлены степени ,
а правые части уравнений – это числа.

Многочлен вида называется Однородным Многочленом степени , если все его члены имеют одинаковую степень, которая равна .

Например, – это однородный многочлен второй степени, а – это однородный многочлен четвертой степени.

Однородные системы решают с помощью использования методов алгебраического сложения и введения новых переменных.

Пример 50. Решите систему уравнений .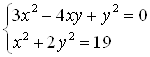

Решение. Проверим, будет ли решение при . Для этого подставим в первое уравнение системы и найдем значение

.

Но если и (из первого уравнения), значит: (из второго уравнения), т. е. – это неверное равенство. Следовательно, – это не корень системы, тогда можно разделить первое уравнение на Получим: .

Обозначим: , получим систему: .

Из первого уравнения системы находим: , . Подставим эти значения во второе уравнение:

А) есл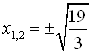и ; и ;

Б) если ; и .

Ответ. .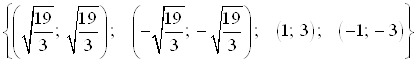

Пример 51. Решите систему .

Решение. Проверим, есть ли решение, если . Подставив во второе уравнение системы, находим: . Значит, имеем два решения: и .

Рассмотрим решения системы, если . Разделим первое уравнение системы на и обозначим . Получим систему:

Из первого уравнения найдем , . Подставим эти значения во второе уравнение и получим: и . Найдем соответствующие значения .

Ответ.

Пример 52. Решите систему .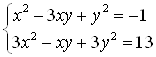

Решение. Умножим первое уравнение на 13 и сложим со вторым уравнением, получим:

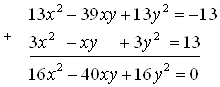
Разделим обе части полученного уравнения на 8, получим: Получили систему уравнений, которая равносильна исходной системе: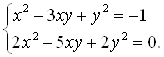

Из второго уравнения видно, что если , то и , но пара не удовлетворяет первому уравнения системы. Поэтому второе уравнение последней системы можно разделить на . Получим:

Пусть

Тогда или .

Получили, что исходная система равносильна совокупности систем: 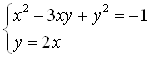и .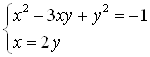

Решения первой системы: .

Решения второй системы:

Ответ. .

Пример 53. Решите систему .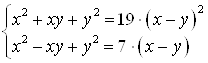

Решение. Приведем систему к виду однородной. Преобразуем первое уравнение: .

Ми получили однородное уравнение. Проверим, будет ли решение, если . Для этого подставим в уравнение системы и найдем значения : если . Так, система имеет решение: .

Если , разделим это уравнение на . Получим:

.

Решаем две системы и находим совокупность решений.

;

.

Ответ. .

< Предыдущая		Следующая >