048. Решение систем нелинейных уравнений

Мы рассмотрели некоторые способы решения систем линейных уравнений. Теперь рассмотрим, какими способами целесообразно решать системы нелинейных уравнений.

Для решения Нелинейных Систем алгебраических уравнений используют такие же методы решения, которые используются для решения систем линейных уравнений:

1) метод подстановки;

2) метод алгебраического сложения;

3) метод замены переменных.

Пример 47. Решите систему методом подстановки.

Решение. Из первого уравнения системы найдем , для этого подставим во второе уравнение системы выражение вместо .

Получим: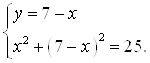

Находим из второго уравнения системы:

.

Система имеет два решения:

А) ; б) .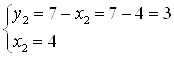

Ответ. .

Пример 48. Решите систему 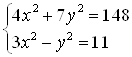методом алгебраического сложения.

Решение. Умножим второе уравнение на 7 и сложим его с первым. Получим , т. е. , .

Подставим в одно из уравнений системы, найдем: .

Ответ. .

Пример 49. Решить систему методом замены переменных.

Решение. Пусть ; 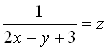. Тогда для и получим систему: .

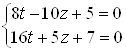Умножим второе уравнение на 2 и сложим с первым. Получим: . Тогда .

Найдем и из системы:

Ответ. .

< Предыдущая		Следующая >