047. Решение систем линейных уравнений

Система уравнений называется Линейной, если все уравнения, которые входят в систему, являются линейными.

Если система линейных уравнений содержит неизвестных, то возможны три случая:

1) система не имеет решения;

2) система имеет только одно решение;

3) система имеет бесконечное множество решений.

Исследовать систему – это значит определить, при каких значениях коэффициентов система имеет единственное решение; не имеет решения; имеет бесконечное множество решений.

Рассмотрим систему линейных уравнений с двумя неизвестными: 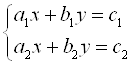, где и – это переменные (неизвестные); , , , – коэффициенты при переменных;
, – свободные члены.

Для решения таких систем часто используют определитель второго порядка.

Определитель второго порядка (главный определитель системы) состоит из коэффициентов при переменных:

Числа , , , называются Элементами определителя.

Элементы , или , , которые расположены по вертикали, образуют Столбцы определителя.

Элементы , или , , которые расположены по горизонтали, образуют Строки определителя.

Элементы , образуют Главную диагональ определителя.

Элементы , образуют Вспомогательную диагональ определителя.

Вспомогательный определитель состоит из коэффициентов при переменных и свободных членов:

; .

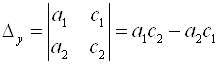Правило Крамера. Если главный определитель системы не равен нулю, то эта система имеет единственное решение:

; .

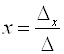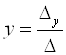В таком случае: ; .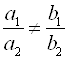

Пример 40. Решите систему .

Решение. Вычислим определители системы:

; ; ;

; .

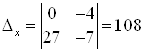Ответ. .

Если главный определитель равен нулю, а хотя бы один вспомогательный определитель не равен нулю, то система не имеет решений (несовместна). Условие несовместимости можно записать так: ; ; ; .

Пример 41. Решите систему .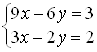

Решение. Вычислим главный определитель системы: .

Свободные члены не пропорциональны коэффициентам при переменных: .

Ответ. Система не имеет решений (несовместна).

Если и главный определитель, и вспомогательные определители равны нулю, то система имеет бесконечное множество решений. Это можно записать так:

; .

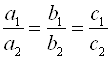Пример 42. Решите систему .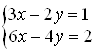

Решение. Вычислим определители системы:

Вычислим отношения между коэффициентами при переменных и свободными членами: . Отношения равны, следовательно, система имеет бесконечное множество решений.

Ответ. Система имеет бесконечное множество решений.

Пример 43. Исследуйте систему .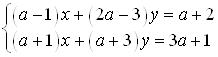

Решение. Коэффициенты системы зависят от параметра .

Запишем главный определитель системы: .

1) Главный определитель будет равен нулю, если и . Поэтому, если и , то система имеет единственное решение.

2) Если то, подставив это значение в систему, получаем: .

Найдем определители этой системы:

Значит, при система не имеет решений (несовместна).

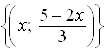3) Если то, подставив это значение в систему, получаем: , поэтому при система имеет бесконечное множество решений вида , где .

Ответ. Если и , то система имеет единственное решение;

Если , то система не имеет решений (несовместна);

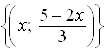Если , то система имеет бесконечное множество решений вида , где .

Рассмотрим систему линейных уравнений с тремя неизвестными: , где , , – это переменные;
, , , , , – коэффициенты при переменных; , , – свободные члены.

Для решения таких систем часто используют определители третьего порядка.

Выражение, обозначенное символом 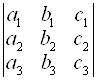, называют Определителем третьего порядка.

Вычислить определитель третьего порядка можно разными способами. Рассмотрим некоторые из них.

1. Произведения элементов главной диагонали и элементов, которые образуют треугольник с основаниями, параллельными главной диагонали, нужно взять со знаком "+". Произведения элементов вспомогательной диагонали и элементов, которые лежат на вершинах треугольников с основаниями, параллельными вспомогательной диагонали, нужно взять со знаком "-" (рис. 4.2).

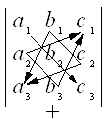
Рисунок 4.2

Например,

2. Определитель третьего порядка можно вычислить по схеме, которая представлена на рисунке 4.3.

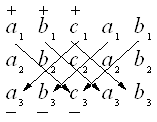
Рисунок 4.3

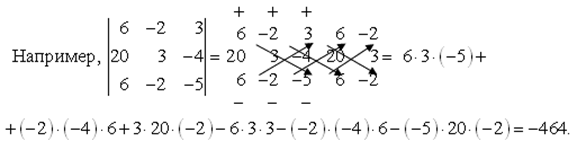
3. Определитель третьего порядка можно разложить по элементам строки или столбца.

Например,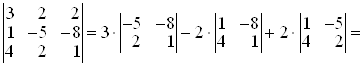

Систему трех линейных уравнений с тремя неизвестными можно решить, используя правило Крамера:

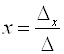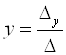; ; , если ; ; ; .

Пример 44. Решите систему уравнений: .

Решение. Вычислим определители системы:

; ;

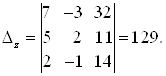
Тогда ; ; .

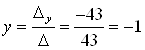Ответ. .

Если система линейных алгебраических уравнений содержит более двух неизвестных, для ее решения удобно использовать Метод Гаусса. Этот метод состоит в последовательном исключении неизвестных.

Рассмотрим использование этого метода с помощью примеров.

Пример 45. Решите систему уравнений .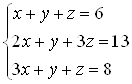

Решение. Умножим первое уравнение системы на 2 и вычтем его из второго уравнения системы. Умножим первое уравнение системы на 3 и вычтем его из третьего уравнения системы. Получим систему уравнений, которая будет равносильна данной: .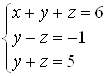

Вычтем из третьего уравнения системы второе, получим: .

Последовательно из третьего, второго и первого уравнений находим:

Ответ. .

Пример 46. Решите систему уравнений: .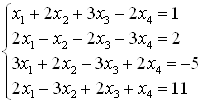

Решение. Используя первое уравнение системы, исключаем неизвестную из второго, третьего и четвертого уравнений. Для этого:

– из второго уравнения вычтем первое уравнение, умноженное на 2;

– из третьего уравнения вычтем первое уравнение, умноженное на 3;

– из четвертого уравнения вычтем первое уравнение, умноженное на 2.

Получим систему уравнений, которая будет эквивалентна исходной:

.

Используем второе уравнение системы и исключим из третьего и четвертого уравнений системы. Для этого из третьего уравнения вычтем второе, умноженное на , а из четвертого уравнения вычтем второе, умноженное на . Получим систему: .

Исключим из четвертого уравнения. Для этого вычтем из него третье уравнение, умноженное на , получим систему: .

Решим полученную треугольную систему и найдем последовательно:

Ответ. .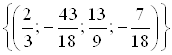

< Предыдущая		Следующая >