043. Уравнения, которые содержат переменную под знаком модуля

Модуль числа обозначается так: .

Определение модуля:

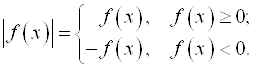
Свойства модуля: ; ; .

Чтобы решить уравнения с переменной под знаком модуля, нужно:

- раскрыть модуль по определению;

- если нужно, то возвести обе части уравнения в квадрат;

- приравнять к нулю выражения, которые стоят под знаком модуля;

- нанести полученные значения на числовую ось (при этом числовая ось разбивается на интервалы или промежутки);

- решить полученные уравнения в каждом из интервалов.

Пример 29. Решите уравнение .

Решение. Раскроем модуль по определению:

А) если , то , тогда , , 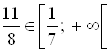значит – это корень уравнения;

Б) если , то , тогда , но , поэтому – это не решение уравнения.

Ответ. .

Пример 30. Решите уравнение .

Решение. Приравняем выражения под знаком модуля к нулю: ; .

Нанесем на числовую ось точки і . Эти точки разделяют числовую ось на три интервала. Обозначим эти интервалы как I, II, III. Найдем знаки выражений под знаком модуля на каждом из интервалов (рис. 4.1).

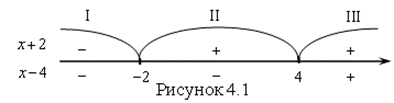
Решаем уравнение на каждом из интервалов.

I. ; , тогда

, но , поэтому на интервале I уравнение решений не имеет.

II. ; , тогда

, но , поэтому на интервале II уравнение решений не имеет.

III. ; , тогда

. , поэтому – это решение уравнения.

Ответ. .

Пример 31. Решите уравнение .

Решение. Это уравнение можно решать методом, который рассмотрен выше. Однако, для данного уравнения с двумя модулями, удобнее использовать свойство модуля и возвести обе части уравнения в квадрат.

Тогда,

.

Ответ. .

< Предыдущая		Следующая >