042. Решение алгебраических уравнений методом введения новой переменной

Для решения алгебраических уравнений часто используют метод введения новой переменной. Рассмотрим это на примерах.

Пример 23. Решите уравнение .

Решение. Пусть , тогда получим уравнение: . Находим ; . Теперь нужно решить два квадратных уравнения:

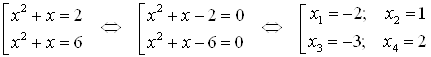
Ответ. .

Пример 24. Решите уравнение .

Решение. Пусть тогда для Получим уравнение: .

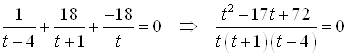Данное уравнение равносильно совокупности уравнений:

, значит и – корни данного уравнения.

Теперь нужно решить два квадратных уравнения:

Ответ. .

Пример 25. Решите уравнение .

Решение. Разделим числитель и знаменатель дроби на получим . Обозначим , тогда для получаем уравнение: , где ; , т. е. ; ; . Теперь нужно решить два уравнения:

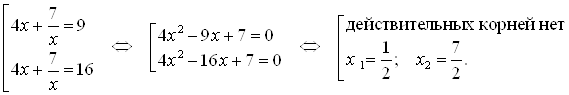
Уравнение не имеет действительных корней, т. к. его дискриминант меньше нуля.

Ответ. .

Уравнение вида можно привести к квадратному, если:

или или .

Пример 26. Решите уравнение .

Решение. В нашем примере , значит, множители левой части можно сгруппировать так:

.

Обозначим тогда:

Получим уравнение:

Теперь решим два квадратных уравнения:

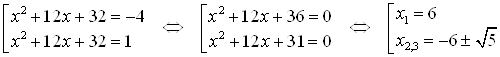
Ответ. .

Уравнение вида приводят к биквадратному уравнению при помощи замены: .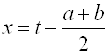

Пример 27. Решите уравнение .

Решение. В нашем примере сделаем замену: .

Тогда: ; . Получаем уравнение для :

.

Раскроем скобки и приведем подобные члены: Получим:

Ответ. .

Уравнение вида называется Возвратным, если , .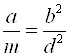

Чтобы решить возвратное уравнение, нужно:

- разделить обе части уравнения на (если , то это не решение уравнения);

- сделать замену переменных и получить квадратное уравнение;

Найти .

Пример 28. Решите уравнение .

Решение. Отношение первого коэффициента к свободному члену и отношение квадрата второго коэффициента к квадрату предпоследнего члена равны между собой: . Разделим исходное уравнение на . Получим . Сгруппируем слагаемые:

.

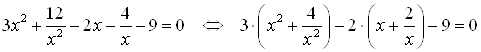Сделаем замену: получим:

Если 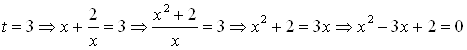, тогда

Если

действительных корней нет.

Ответ. .

< Предыдущая		Следующая >