041. Симметричные уравнения третьей и четвертой степеней

Рациональное уравнение третьей степени называется симметричным, если оно имеет вид: .

Многочлен левой части такого уравнения легко разложить на множители и получить совокупность линейного и квадратного уравнений:

.

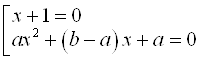Пример 21. Решите уравнение .

Решение. С помощью эквивалентных преобразований разложим левую часть уравнения на множители:

.

Приравняем каждый множитель к нулю:

.

Ответ. .

Рациональное уравнение четвертой степени называется симметричным, если оно имеет вид: .

Пример 22. Решите уравнение .

Решение.

.

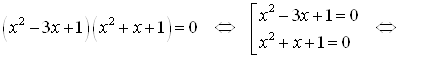
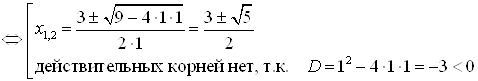
Ответ. .

< Предыдущая		Следующая >